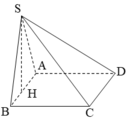
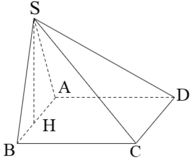
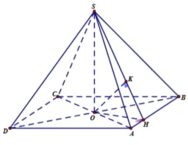
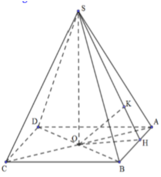
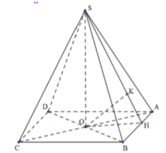
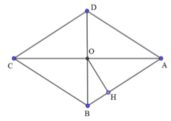
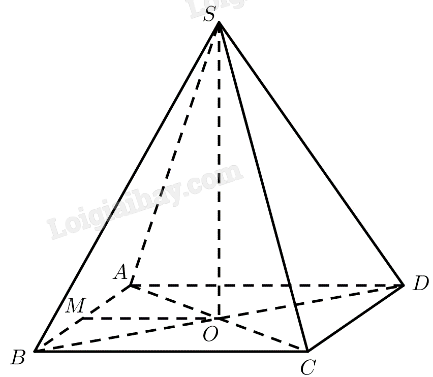
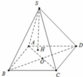
Cho hình chóp S.ABCD có đáy là hình thoi ABCD. AC cắt BD tại gốc tọa độ O. Biết \(A\left(2;0;0\right),B\left(0;1;0\right),S\left(0;0;2\sqrt{2}\right)\). Gọi M là trung điểm cạn SC
a) Viết phương trình mặt phẳng SA và song song với BM
b) Tính khoảng cách giữa hai đường thẳng SA và BM