Trong không gian Oxyz hãy viết phương trình mặt cầu đi qua bốn điểm \(A\left(1;0;0\right);B\left(0;-2;0\right);C\left(0;0;4\right)\) và gốc tọa độ. Hãy xác định tâm và bán kính của mặt cầu đó ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 11 2019
Phương trình mặt cầu (S) cần tìm có dạng: x 2 + y 2 + z 2 – 2ax – 2by – 2cz + d = 0.
Vì
A ∈ (S) nên ta có: 1 – 2a + d =0 (1)
B ∈ (S) nên ta có: 4 + 4b + d = 0 (2)
C ∈ (S) nên ta có: 16 – 8c + d = 0 (3)
D ∈ (S) nên ta có: d = 0 (4)
Giải hệ 4 phương trình trên ta có: d = 0, a = 1/2, b = −1,c = 2.
Vậy mặt cầu (S) cần tìm có phương trình là: x 2 + y 2 + z 2 –x + 2y – 4z = 0
Phương trình mặt cầu (S) có thể viết dưới dạng:
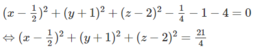
Vậy mặt cầu (S) có tâm I(1/2; -1; 2) và có bán kính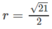 
CM
14 tháng 4 2017
Đáp án D
Phương trình tổng quát của mặt cầu (S) có dạng x 2 + y 2 + z 2 - 2ax - 2by - 2cz + d = 0 với a 2 + b 2 + c 2 - d > 0
Ta có: O(0; 0; 0) ∈ (S) ⇔ d = 0
A(-4; 0; 0) ∈ (S) ⇔ ( - 4 ) 2 + 0 2 + 0 2 - 2a.(-4) - 0 - 0 + 0 = 0 ⇔ a = -2
B(0; 2; 0) ∈ (S) ⇔ 0 2 + 2 2 + 0 2 - 0 - 2b.2 - 0 + 0 = 0 ⇔ b = 1
C(0; 0; 4) ∈ (S) ⇔ 0 2 + 0 2 + 4 2 - 0 - 0 - 2c.4 - 0 = 0 ⇔ c = 2
Vậy phương trình tổng quát của mặt cầu (S) là: x 2 + y 2 + z 2 + 4x -2y - 4z = 0
CM
6 tháng 12 2019
Đáp án A
Ta có I M = 2 − 1 2 + 2 − 0 2 + − 1 + 3 2 = 3 . Mặt cầu (S) có tâm I 1 ; 0 ; − 3 và bán kính R = I M = 3 nên có phương trình là x − 1 2 + y 2 + z + 3 2 = 9 .
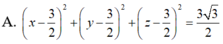
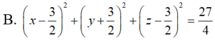
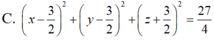
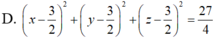
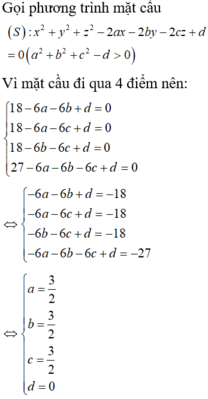
Phương trình mặt cầu (S) cần tìm có dạng :
\(x^2+y^2+z^2-2ax-2by-2cz+d=0\)
Vì \(A\in\left(S\right)\) nên ta có : \(1-2a+d=0\left(1\right)\)
\(A\in\left(S\right)\) nên ta có : \(4+4b+d=0\left(2\right)\)