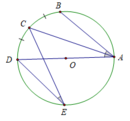
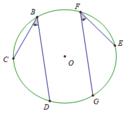
cách chứng minh góc chắn cung bằng nủa góc nội tiếp mà ko dùng kiến thức HKI lớp 9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 8 2023
góc tạo bởi tia tiếp tuyến và dây cung bằng một nửa số đo cung bị chắn
góc nội tiếp chắn cung cũng bằng một nửa số đo cung bị chắn
=>góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau
CM
18 tháng 11 2017
(A) Sai. Góc nội tiếp là góc có đỉnh nằm trên đường tròn, hai cạnh chứa hai dây cung của đường tròn đó.
(B) Sai. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung hoặc chắn hai cung bằng nhau.
(C) Sai. Trong một đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau.
(D) Sai. Trong một đường tròn, số đo của góc nội tiếp bằng một nửa số đo của góc ở tâm cùng chắn một cung.
(E) Đúng. Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
16 tháng 10 2023
Gọi K là trung điểm của HD
Xét ΔHDC có
K,M lần lượt là trung điểm của HD,HC
=>KM là đường trung bình của ΔHDC
=>KM//DC và \(KM=\dfrac{DC}{2}\)
mà \(AB=\dfrac{DC}{2}\)
nên KM=AB
KM//DC
DC//AB
Do đó: KM//AB
Xét tứ giác ABMK có
AB//MK
AB=MK
Do đó: ABMK là hình bình hành
=>AK//BM
Xét ΔADM có
MK,DH là đường cao
MK cắt DH tại K
Do đó: K là trực tâm
=>\(AK\perp DM\)
mà AK//BM
nên \(BM\perp DM\)
11 tháng 11 2021
a, Vì \(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\) nên AMBO nội tiếp
Hay A,B,M,O cùng thuộc 1 đg tròn
CM
3 tháng 6 2017
a) Đúng (theo hệ quả b).
b) Sai. Vì trong cùng một đường tròn, các góc nội tiếp cùng chắn 1 cung hoặc chắn các cung bằng nhau thì bằng nhau.
Trong một đường tròn, các góc nội tiếp bằng nhau chưa chắc cùng chắn một cung.
Kiến thức áp dụng
Định lý: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
Hệ quả: Trong một đường tròn, các góc nội tiếp bằng nhau chắn các cung bằng nhau.