Tìm số phức \(z\) biết
a) \(\overline{z}=z^3\)
b) \(\left|z\right|+z=3+4i\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đặt \(z=x+yi\)
\(\left|x+yi+x-yi+2\right|+2\left|x+yi-x+yi-2i\right|\le12\)
\(\Leftrightarrow\left|2x+2\right|+4\left|\left(y-1\right)i\right|\le12\)
\(\Leftrightarrow\left|x+1\right|+2\left|y-1\right|\le6\)
Tập hợp z là miền trong hình thoi (gồm cả biên) với 4 đỉnh: \(A\left(-7;1\right)\) ; \(B\left(-1;4\right)\) ; \(C\left(5;1\right)\) ; \(D\left(-1;-2\right)\)
\(P^2=\left|z-4-4i\right|^2=\left(x-4\right)^2+\left(y-4\right)^2\) có tập hợp là đường tròn (C) tâm \(I\left(4;4\right)\) bán kính \(R=P>0\) sao cho (C) và hình thoi ABCD có ít nhất 1 điểm chung
Từ hình vẽ ta thấy \(P_{max}\) khi (C) đi qua A \(\Rightarrow P=IA\) và \(P_{min}\) khi (C) tiếp xúc BC \(\Rightarrow P=d\left(I;BC\right)\)
\(\overrightarrow{IA}=\left(-11;-3\right)\Rightarrow M=IA=\sqrt{130}\)
\(\overrightarrow{BC}=\left(6;-3\right)\Rightarrow\) đường thẳng BC nhận (1;2) là 1 vtpt
Phương trình BC: \(1\left(x+1\right)+2\left(y-4\right)=0\Leftrightarrow x+2y-7=0\)
\(\Rightarrow m=d\left(I;BC\right)=\dfrac{\left|4+2.4-7\right|}{\sqrt{1^2+2^2}}=\sqrt{5}\)
\(\Rightarrow M+m=\sqrt{130}+\sqrt{5}\)

a) Ta có z. z = z 2 nên từ z = z 3 ⇒ z 2 = z 4
Đặt z = a+ bi , suy ra:
a 4 + b 4 − 6 a 2 b 2 + 4ab( a 2 − b 2 )i = a 2 + b 2 (∗)
Do đó, ta có: 4ab( a 2 − b 2 ) = 0 (∗∗)
Từ (∗∗) suy ra các trường hợp sau:
+) a = b = 0 ⇒ z = 0
+) a = 0, b ≠ 0: Thay vào (∗), ta có b 4 = b 2 ⇒ b = 1 hoặc b = -1 ⇒ z = i hoặc z = -1
+) b = 0, a ≠ 0: Tương tự, ta có a = 1 hoặc a = -1 ⇒ z = 1 hoặc z = -1
+) a ≠ 0, b ≠ 0 ⇒ a 2 − b 2 = 0⇒ a 2 = b 2 , thay vào (∗) , ta có:
2 a 2 (2 a 2 + 1) = 0, không có a nào thỏa mãn (vì a ≠ 0 )
b) Đặt z = a + bi. Từ |z| + z = 3 + 4i suy ra
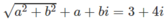
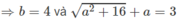
⇒ a 2 + 16 = ( 3 - a ) 2 = 9 − 6a + a 2
⇒ 6a = −7 ⇒ a = −7/6
Vậy z = −7/6 + 4i

Lời giải:
Đặt \(z=a+bi\). Ta có: \(|z|\leq 2\Leftrightarrow a^2+b^2\leq 4\)
Có:
\(p=2|z+1|+2|z-1|+|z-\overline{z}-4i|\)
\(=2|(a+1)+bi|+2|(a-1)+bi|+|(a+bi)-(a-bi)-4i|\)
\(=2\sqrt{(a+1)^2+b^2}+2\sqrt{(a-1)^2+b^2}+\sqrt{(2b-4)^2}\)
\(=2\sqrt{(a+1)^2+b^2}+\sqrt{(a-1)^2+b^2}+4-2b\)
(do \(a^2+b^2\leq 4\Rightarrow b^2\leq 4\Rightarrow b\leq 2\Rightarrow \sqrt{(2b-4)^2}=4-2b\) )
\(\Leftrightarrow p=2[\sqrt{(a+1)^2+b^2}+\sqrt{(a-1)^2+b^2}-b+2]\)
Theo BĐT Mincopxky :
\(p\geq 2(\sqrt{(a+1+1-a)^2+(b+b)^2}-b+2)\)
\(\Leftrightarrow p\geq 2(2\sqrt{b^2+1}-b+2)\)
Xét \(f(b)=2\sqrt{b^2+1}-b+2\) với \(b\in [-2;2]\)
Có: \(f'(b)=\frac{2b}{\sqrt{b^2+1}}-1=0\Leftrightarrow b=\pm \frac{\sqrt{3}}{3}\)
Lập bảng biến thiên ta suy ra \(f(b)_{\min}=f(\frac{\sqrt{3}}{3})=2+\sqrt{3}\)
\(\Rightarrow p\geq 2f(b)\geq 2(2+\sqrt{3})\)
Vậy \(p_{\min}=4+2\sqrt{3}\)
Dấu bằng xảy ra khi \(b=\frac{\sqrt{3}}{3}; \frac{a+1}{1-a}=\frac{b}{b}=1\Rightarrow a=0\)

Đặt \(z=x+yi\)
\(\Rightarrow\sqrt{x^2+y^2}+x+yi=3+4i\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x^2+y^2}+x=3\\y=4\end{matrix}\right.\)
\(\Rightarrow\sqrt{x^2+16}+x=3\Leftrightarrow\sqrt{x^2+16}=3-x\) (\(x\le3\))
\(\Leftrightarrow x^2+16=x^2-6x+9\Rightarrow6x=-7\Rightarrow x=-\frac{7}{6}\)
\(\Rightarrow z=-\frac{7}{6}+4i\)