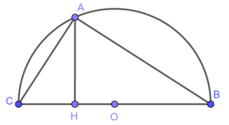
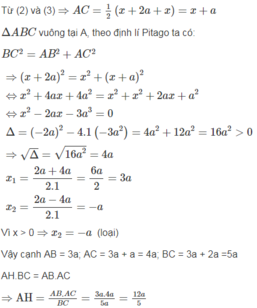tìm tất cả các tam giác ABC có độ dài các cạnh là các số nguyên dương thỏa mãn độ dài cạnh AC bằng độ dài đường phân giác trong góc A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 6 2019
Ta có:
\(\frac{1}{AB}+\frac{1}{AC}+\frac{1}{AH}=1\)
\(\Leftrightarrow\frac{1}{AB^2}+\frac{1}{AC^2}+\frac{1}{AH^2}+\frac{2}{AB.AC}+\frac{2}{AC.AH}+\frac{2}{AB.AH}=1\)
\(\Leftrightarrow\frac{2}{AH^2}+\frac{2}{AH.BC}+\frac{2}{AC.AH}+\frac{2}{AB.AH}=1\)(Do \(\hept{\begin{cases}\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\\AB.AC=AH.BC\end{cases}}\)(Hệ thức lượng)
\(\Leftrightarrow\frac{2}{AH}\left(\frac{1}{AH}+\frac{1}{BC}+\frac{1}{AB}+\frac{1}{AC}\right)=1\)
\(\Leftrightarrow\frac{2}{AH}\left(1+\frac{1}{BC}\right)=1\)(Do \(\frac{1}{AB}+\frac{1}{AC}+\frac{1}{AH}=1\))
\(\Leftrightarrow\frac{BC+1}{BC}=\frac{AH}{2}\)
\(\Leftrightarrow2\left(BC+1\right)=AH.BC\)
\(\Leftrightarrow4BC+4=2AB.AC\)(Do AH.BC = AB.AC)
Kết hợp với Py-ta-go trong tam giác vuông ABC: \(BC^2=AB^2+AC^2\)
\(\Rightarrow BC^2+4BC+4=AB^2+2AB.AC+AC^2\)
\(\Leftrightarrow\left(BC+2\right)^2=\left(AB+AC\right)^2\)
\(\Leftrightarrow AB+AC=BC+2\)(Do \(\hept{\begin{cases}BC+2>0\\AB+AC>0\end{cases}}\))
Mà 3 cạnh AB,AC,BC là 3 cạnh nguyên lớn hơn 0
=> Chỉ có 2 cặp (AB,AC,BC) thỏa mãn: \(\left(3,4,5\right),\left(4,3,5\right)\)
CM
27 tháng 2 2019
Đặt độ dài cạnh AB = x; điều kiện: x > 0
Theo bài ra theo điều (1) ta có: BC = x + 2a (3)
