Question

[Duong Thi Nhuong]

Giải dùm mk hệ phương trình này vs

Answer 1

[Eren]

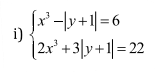
\(\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\)

\(\Leftrightarrow\dfrac{6}{2x}+\dfrac{6}{y}=\dfrac{1}{4}\)

\(\Leftrightarrow6\left(\dfrac{1}{2x}+\dfrac{1}{y}\right)=\dfrac{1}{4}\)

\(\Leftrightarrow\dfrac{1}{2x}+\dfrac{1}{y}=\dfrac{1}{24}^{\left(1\right)}\)

Lại có: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}^{\left(2\right)}\)

Lấy ⁽²⁾ trừ ⁽¹⁾ ta có:

\(\dfrac{1}{x}+\dfrac{1}{y}-\dfrac{1}{2x}-\dfrac{1}{y}=\dfrac{1}{16}-\dfrac{1}{24}\)

\(\Leftrightarrow\dfrac{2-1}{2x}=\dfrac{1}{48}\)

\(\Leftrightarrow\dfrac{1}{2x}=\dfrac{1}{48}\)

=> 2x = 48

<=> x = 24

Thay x = 24 vào ⁽²⁾ ta có:

\(\dfrac{1}{24}+\dfrac{1}{y}=\dfrac{1}{16}\)

\(\Leftrightarrow\dfrac{1}{y}=\dfrac{1}{48}\)

=> y = 48

Vậy ...

Answer 2

[Mỹ Duyên]

Ta có: \(\dfrac{3}{x}\) + \(\dfrac{6}{y}\) = \(\dfrac{1}{4}\)

<=> 3(\(\dfrac{1}{x}\) + \(\dfrac{2}{y}\) ) = \(\dfrac{1}{4}\)

<=> \(\dfrac{1}{x}\) + \(\dfrac{2}{y}\) = \(\dfrac{1}{12}\) (1)

Mặt khác: \(\dfrac{1}{x}\) + \(\dfrac{1}{y}\) = \(\dfrac{1}{16}\) (2)

Trừ (2) cho (1) vế theo vế ta được:

\(\dfrac{1}{x}\) + \(\dfrac{2}{y}\) - \(\dfrac{1}{x}\) - \(\dfrac{1}{y}\) = \(\dfrac{1}{12}\) - \(\dfrac{1}{16}\)

<=> \(\dfrac{1}{y}\) = \(\dfrac{1}{48}\) <=> y = 48

Thay y =48 vào (2) ta có: \(\dfrac{1}{x}\) + \(\dfrac{1}{48}\) = \(\dfrac{1}{16}\)

<=> \(\dfrac{1}{x}\) = \(\dfrac{1}{24}\) <=> x = 24

Vậy x =24 ; y =48