Một chất điểm chuyển động theo quy luật \(s=6t^2-t^3\). Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 6 2017
Xét hàm số s = t 2 - 1 6 t 3 .
Vận tốc của chuyển động là v = y ' = 2 t - 1 2 t 2 .
Ta có v' = 2 - t; v' = 0 nên t = 2
Lập bảng biến thiên và suy ra m a x v t ∈ 0 ; + ∞ = 8 3 ⇔ t = 2
Đáp án C
CM
5 tháng 11 2019
s = 6 t 2 − t 3 , t > 0
Vận tốc chuyển động là v = s’ , tức là v = 12t – 3 t 2
Ta có: v’ = 12 – 6t
v’ = 0 ⇔ t = 2
Hàm số v đồng biến trên khoảng (0;2) và nghịch biến trên khoảng (2;+ ∞ ).
Vận tốc đạt giá trị lớn nhất khi t = 2. Khi đó max V = V C Đ = v(2) = 12(m/s).
CM
14 tháng 12 2018
s = 6 t 2 – t 3 , t > 0
Vận tốc chuyển động là v = s’ , tức là v = 12t – 3 t 2
Ta có: v’ = 12 – 6t
v’ = 0 ⇔ t = 2
Hàm số v đồng biến trên khoảng (0;2) và nghịch biến trên khoảng (2;+ ∞ ).
Vận tốc đạt giá trị lớn nhất khi t = 2. Khi đó max V = V CD = v(2) = 12(m/s).
CM
1 tháng 10 2019
Đáp án A
Ta có v = S ' = 24 t - 6 t 2 = - 6 ( t - 2 ) 2 + 24 ≤ 24 ( m / s ) ⇒ v m a x = 24 m / s đạt được khi t=2(giây)
CM
2 tháng 11 2019
Chọn A.
Vận tốc của chuyển động là v = s' tức là 
Bảng biến thiên:
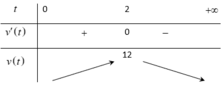
Hàm số v(t) đồng biến trên khoảng (0;2) và nghịch biến trên khoảng (2;+∞)
⇔ Max v(t) = 12 khi t = 2.
Vận tốc đạt giá trị lớn nhất bằng 12 khi t = 2(s).
CM
29 tháng 10 2017
Đáp án A
Phương trình vận tốc của vật: v = S ' t = 12 t − 3 t 2 = − 3 t − 2 2 + 12 ≤ 12
Do đó vận tốc đạt giá trị lớn nhất khi t = 2 s
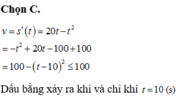
Vận tóc của chuyển động là:
\(v=s'=12t-3t^2\)
Ta có \(v'=12-6t\)
\(v'=0\) khi t = 2 và \(v'\) đổi dấu từ dương sang âm khi đi qua t=2. Vậy \(v\) đạt giá trị lớn nhất khi t = 2.