Hãy so sánh :388 và 559
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{111}{115}\)= 1 - \(\frac{4}{115}\)
\(\frac{555}{559}\)= 1 - \(\frac{4}{559}\)
\(\frac{4}{115}\)> \(\frac{4}{559}\)
=> \(\frac{111}{115}\) < \(\frac{555}{559}\)

Ta có:
\(\frac{111}{115}=\frac{111.5}{115.5}=\frac{555}{575}< \frac{555}{559}\)
=> \(\frac{111}{115}< \frac{555}{559}\)

111/115= 1 - 4/115
555/559= 1- 4/559
Vì: 4/115> 4/559
=> 1- 4/115< 1- 4/559
=> 111/115< 555/559



B=\(\frac{12}{2^2.4^2}+\frac{20}{4^2.6^2}+......+\frac{388}{96^2.98^2}+\frac{396}{98^2.100^2}\)
=\(\frac{1}{2^2}-\frac{1}{4^2}+\frac{1}{4^2}-\frac{1}{6^2}+...+\frac{1}{96^2}-\frac{1}{98^2}+\frac{1}{98^2}-\frac{1}{100^2}\)
=\(\frac{1}{2^2}-\frac{1}{100^2}\)
=\(\frac{2599}{10000}< \frac{2500}{10000}=\frac{1}{4}\)
=> B<\(\frac{1}{4}\)

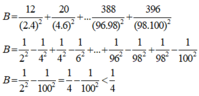
B=\(\frac{12}{\left(2.4\right)^2}\)+\(\frac{20}{\left(4.6\right)^2}\)+.....+\(\frac{396}{\left(98.100\right)^2}\)
B=\(\frac{4^2-2^2}{2^2.4^2}\)+ \(\frac{6^2-4^2}{4^2.6^2}\)+....+\(\frac{100^2-98^2}{\left(98^2.100^2\right)}\)
B=\(\frac{1}{2^2}\)-\(\frac{1}{4^2}\)+\(\frac{1}{4^2}\)-\(\frac{1}{6^2}\)+....+\(\frac{1}{98^2}\)-\(\frac{1}{100^2}\)
B=\(\frac{1}{2^2}\)-\(\frac{1}{100^2}\)< \(\frac{1}{2^2}\)=\(\frac{1}{4}\)
Vậy B<\(\frac{1}{4}\)