Trên đường cong \(y=4x^2-6x+3\), hãy tìm điểm tại đó tiếp tuyến song song với đường thẳng \(y=2x\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 7 2023
a:Sửa đề: y=x^3-3x^2+2
y'=3x^2-3*2x=3x^2-6x
y=2
=>x^3-3x^2=0
=>x=0 hoặc x=3
=>y'=0 hoặc y'=3*3^2-6*3=27-18=9
A(0;2); y'=0; y=2
Phương trình tiếp tuyến có dạng là;
y-2=0(x-0)
=>y=2
A(3;2); y'=9; y=2
Phương trình tiếp tuyến có dạng là:
y-2=9(x-3)
=>y=9x-27+2=9x-25
b: Tiếp tuyến tại M song song với y=6x+1
=>y'=6
=>3x^2-6x=6
=>x^2-2x=2
=>x=1+căn 3 hoặc x=1-căn 3
=>y=0 hoặc y=0
M(1+căn 3;0); y=0; y'=6
Phương trình tiếp tuyến là:
y-0=6(x-1-căn 3)=6x-6-6căn3
M(1-căn 3;0); y=0; y'=6
Phương trình tiếp tuyến là:
y-0=6(x-1+căn 3)
=>y=6x-6+6căn 3
CM
3 tháng 11 2017
Chọn C.
Đạo hàm: y’ = 3x2 + 6x – 8.
Tiếp tuyến cần tìm song song với đường thẳng Δ: y = x + 2017 nên hệ số góc của tiếp tuyến là 1.
Ta có phương trình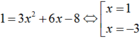 
Tại M(1; -3). Phương trình tiếp tuyến là y = x – 4.
Tại N(-3; 25). Phương trình tiếp tuyến là y = x + 28.
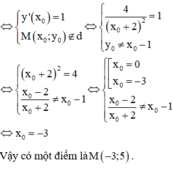
Lời giải
Tiếp tuyến có dạng t: y=ax+b
Để tiếp tuyến // với y=2x =>a=2
đường thẳng tiếp tuyến có dạng t: y=2x+b
là tiếp tuyến của (C) \(y=4x^2-6x+3\)
Thì \(\Rightarrow pt:=4x^2-6x+3=2x+b\) phải có nghiệm kép
\(\Leftrightarrow4x^2-8x+3-b=0\) phải có nghiệm kép
\(\Rightarrow\Delta=0\Rightarrow16-4\left(3-b\right)=4b+4=0\Rightarrow b=-1\)
\(4x^2-8x+4=\left(x-1\right)^2=0\Rightarrow x=1\)\(\)
với x=1 ta có y(1) =2.1-1=1
Vậy điểm cần tìm là : A(1,1)
Có \(y'\left(x\right)=8x-6\).
Nếu \(y'\left(x_0\right)\) là hệ số góc của tiếp tuyến và tiếp tuyến song song với đường thẳng \(y=2x\) suy ra: \(8x-6=2\)\(\Leftrightarrow x=1\).
Vậy tiếp tuyến cần tìm có phương trình:
\(y=2\left(x-1\right)+y\left(1\right)\)\(\Leftrightarrow y=2x-2+1\)\(\Leftrightarrow y=2x-1\).