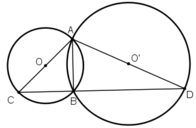
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ các đường kính AC và AD của hai đường tròn. Chứng minh rằng ba điểm C, B, D thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


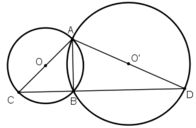
Trong đường tròn tâm O, 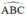 là góc nội tiếp chắn nửa đường tròn
là góc nội tiếp chắn nửa đường tròn
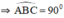
Trong đường tròn tâm O’,  là góc nội tiếp chắn nửa đường tròn
là góc nội tiếp chắn nửa đường tròn
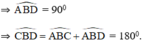
Suy ra, ba điểm C, B và D thẳng hàng.

Trong đường tròn tâm O, 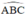 là góc nội tiếp chắn nửa đường tròn
là góc nội tiếp chắn nửa đường tròn
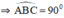
Trong đường tròn tâm O’,  là góc nội tiếp chắn nửa đường tròn
là góc nội tiếp chắn nửa đường tròn
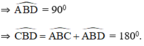
Suy ra, ba điểm C, B và D thẳng hàng.
Kiến thức áp dụng
+ Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông.

1: Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{ABC}=90^0\)
Xét (O') có
\(\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{ABD}=90^0\)
Ta có: \(\widehat{ABC}+\widehat{ABD}=\widehat{CBD}\)
\(\Leftrightarrow\widehat{CBD}=90^0+90^0=180^0\)
hay C,B,D thẳng hàng(đpcm)

a: góc ABC=1/2*sđ cung AC=90 độ
góc ABD=1/2*180=90 độ
góc CBD=góc ABC+góc ABD=90+90=180 độ
=>C,B,D thẳng hàng
b: góc AFC=1/2*sđ cung AC=90 độ
=>CF vuông góc AD
góc AED=1/2*180=90 độ
=>DE vuông góc AC
góc CED=góc CFD=90 độ
=>CEFD nội tiếp

ta có: góc ABC = 90 độ ( góc nt chắn nửa đt )
góc ABD = 90 độ ( góc nt chắn nửa đt )
=> CBD = góc ABC + góc ABD = 180 độ
=> ba điểm C,B,D thẳng hàng
hình bẹn tự vẽ hén:
giải:
Có \(\widehat{ABC}=90^o\) ( vì góc ABC chắn nửa đường tròn đường kính AC)
\(\widehat{ABD}=90^o\) ( vì góc ABD chắn nửa đường tròn đường kính AD)
\(\Rightarrow\widehat{ABC}+\widehat{ABD}=180^o\)
Vậy ba điểm C; B ; D thẳng hàng.

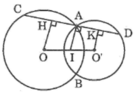
Kẻ OH ⊥ CD, O’K ⊥ CD
Ta có: IA ⊥ CD
Suy ra : OH // IA // O’K
Theo giả thiết : IO = IO’
Suy ra : AH = AK (tính chất đường thẳng song song cách đều) (1)
Ta có : OH ⊥ AC
Suy ra : HA = HC = (1/2).AC (đường kính dây cung) ⇒ AC = 2AH (2)
Lại có : O’K ⊥ AD
Suy ra : KA = KD = (1/2).AD (đường kính dây cung) ⇒ AD = 2AK (3)
Từ (1), (2) và (3) suy ra: AC = AD
Nối B với 3 điểm A, C, D ta có:
(góc nội tiếp chắn nửa đường tròn)
( góc nội tiếp chắn nửa đường tròn)
Vậy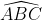 +
+ 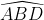 =
= 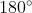
Suy ra ba điểm A, C, D thẳng hàng.