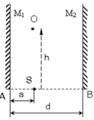
Cho hai gương phẳng M, N hợp với nhau một góc vuôn, quay mặt phản xạ vào nhau. Có hai điểm A và B nằm trong hai gương phẳng.
a) Nêu cách vẽ tia sáng xuất phát từ A, đến gương M tại I, phản xạ đến gương N tại K rồi phản xạ tiếp đến điểm B.
b) Chứng minh AI // BK



a) Vẽ ảnh ảo A' đối xứng với A qua gương M
Vẽ ảnh ảo A" đối xứng A qua gương N
Nối từ A" tới B cắt gương N tại K
Nối từ A' đến K cắt gương M tại I
Nối từ A đến I ta có Tia sáng AIKB xuất phát từ A và đi qua điểm B
b)Ta có
\(\widehat{AIH}=\widehat{HKN}\)(mk giải thích thêm là Vì AIH=HIK;HIK=IKO vì cùng phụ với IKP nên suy ra vậy đó)
Mà \(\widehat{HKN}=\widehat{IHK}\)(cùng phụ với PKH)
Suy ra \(\widehat{AIH}=\widehat{IHK}\)
Mà 2 góc này ở vị trí so le trong suy ra:
\(AI\)//BK
a) Do tia sáng AI từ A đến gương M sẽ có tia phản xạ kéo dài đi qua ảnh ảo của điểm A qua gương M. Để tia sáng này đi đến gương N tại K và phản xạ đến B thì đồng nghĩa với tia tới IK phải có đường kéo dài đi qua ảnh ảo của điểm B trên gương N.
Từ đó ta có cách vẽ:
- Vẽ hai ảnh ảo A' và B' của hai điểm A và B trên hai gương.
- Ta nối hai điểm A' và B', đoạn thẳng này cắt gương M tại I và cắt gương N tại K.
- AIKB là tia sáng cần vẽ.
b) Kẻ hai pháp tuyến của đường truyền ánh sáng AIK và đường truyền ánh sáng IKB, Hai pháp tuyến này cắt nhau tại O.
Theo định luật phản xạ ánh sáng:
\(\widehat{AIK}=i_1+i_2=2i_2;;\widehat{IKB}=k_1+k_2=2k_2\\ \Rightarrow\widehat{AIK}+\widehat{IBK}=2i_2+2k_2=2\left(i_2+k_2\right)\)
Xét \(\Delta IOK\) vuông tại O \(\Rightarrow i_2+k_2=90^o\) từ đó suy ra:
\(\widehat{AIK}+\widehat{IBK}=2.90^o=180^o\)
Ta có đoạn thẳng IK cắt hai đường thẳng AI, BK và tạo thành 2 góc trong cùng phía có tổng số đo là 180o (2 góc bù nhau) nên AI//BK.