Cho hai hàm số \(y=f\left(x\right)\) và \(y=g\left(x\right)\) cùng xác định trên khoảng \(\left(-\infty

SG

Sách Giáo Khoa

10 tháng 4 2017

Cho hai hàm số \(y=f\left(x\right)\) và \(y=g\left(x\right)\) cùng xác định trên khoảng \(\left(-\infty;a\right)\). Dùng định nghĩa chứng minh rằng...

Đọc tiếp

#Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 5 2022

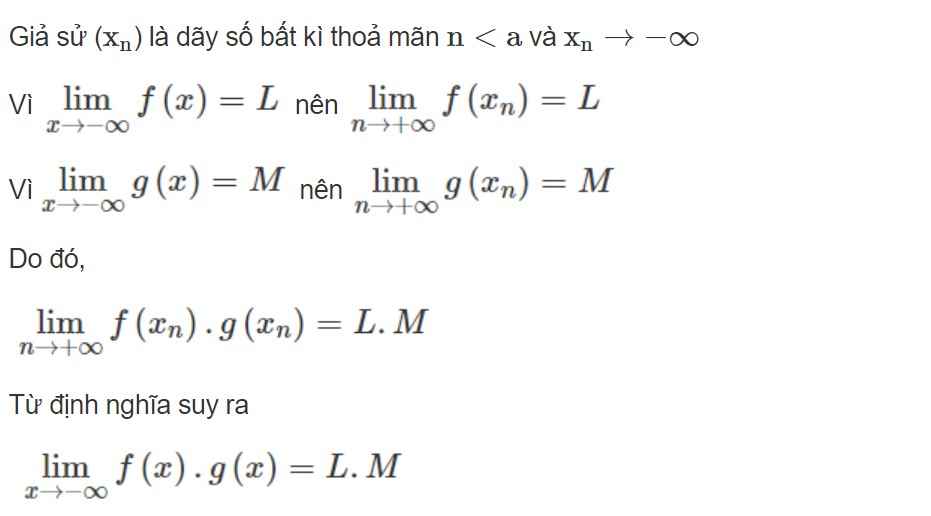
undefined

Đúng(0)

B

Buddy

17 tháng 7 2023

Cho hai hàm số \(y = f\left( x \right) = \frac{1}{{x - 1}}\) và \(y = g\left( x \right) = \sqrt {4 - x} \).

a) Tìm tập xác định của mỗi hàm số đã cho.

b) Mỗi hàm số trên liên tục trên những khoảng nào? Giải thích.

#Toán lớp 11

1

HQ

Hà Quang Minh

Giáo viên

22 tháng 9 2023

a) • \(y = f\left( x \right) = \frac{1}{{x - 1}}\)

ĐKXĐ: \(x - 1 \ne 0 \Leftrightarrow x \ne 1\)

Vậy hàm số có tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).

• \(y = g\left( x \right) = \sqrt {4 - x} \)

ĐKXĐ: \(4 - x \ge 0 \Leftrightarrow x \le 4\)

Vậy hàm số có tập xác định: \(D = \left( { - \infty ;4} \right]\).

b) • Với mọi \({x_0} \in \left( { - \infty ;1} \right)\), ta có:

\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{1}{{x - 1}} = \frac{{\mathop {\lim }\limits_{x \to {x_0}} 1}}{{\mathop {\lim }\limits_{x \to {x_0}} x - \mathop {\lim }\limits_{x \to {x_0}} 1}} = \frac{1}{{{x_0} - 1}} = f\left( {{x_0}} \right)\)

Vậy hàm số \(y = f\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( { - \infty ;1} \right)\).

Tương tự ta có hàm số \(y = f\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( {1; + \infty } \right)\).

Ta có: Hàm số không xác định tại điểm \({x_0} = 1\)

\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{1}{{x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \frac{1}{{x - 1}} = - \infty \)

Vì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\).

Vậy hàm số \(y = f\left( x \right)\) không liên tục tại điểm \({x_0} = 1\).

• Với mọi \({x_0} \in \left( { - \infty ;4} \right)\), ta có:

\(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \sqrt {4 - x} = \sqrt {\mathop {\lim }\limits_{x \to {x_0}} 4 - \mathop {\lim }\limits_{x \to {x_0}} x} = \sqrt {4 - {x_0}} = g\left( {{x_0}} \right)\)

Vậy hàm số \(y = g\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( { - \infty ;4} \right)\).

Ta có: \(g\left( 4 \right) = \sqrt {4 - 4} = 0\)

\(\mathop {\lim }\limits_{x \to {4^ - }} g\left( x \right) = \mathop {\lim }\limits_{x \to {4^ - }} \sqrt {4 - x} = \sqrt {\mathop {\lim }\limits_{x \to {4^ - }} 4 - \mathop {\lim }\limits_{x \to {4^ - }} x} = \sqrt {4 - 4} = 0 = g\left( 4 \right)\)

Vậy hàm số \(y = g\left( x \right)\) liên tục tại điểm \({x_0} = 4\).

Hàm số không xác định tại mọi \({x_0} \in \left( {4; + \infty } \right)\) nên hàm số \(y = g\left( x \right)\) không liên tục tại mọi điểm \({x_0} \in \left( {4; + \infty } \right)\).

Vậy hàm số \(y = g\left( x \right)\) liên tục trên nửa khoảng \(\left( { - \infty ;4} \right]\).

Đúng(0)

NL

Nguyễn Lê Phước Thịnh

11 tháng 11 2023

Câu 48: Cho hàm số y=f(x) có đạo hàm liên tục trên R và \(f'\left(x\right)=x\left(2x-1\right)\left(x^2+3\right)+2\). Hàm số \(y=f\left(3-x\right)+2x+2023\) đồng biến trên khoảng nào trong các khoảng sau?A: \(\left(-\infty;3\right)\)B: (3;5)C: (2;5/2)D: (5/2;3)Câu 50: Cho hàm số y=f(x) có đạo hàm \(f'\left(x\right)=\left(x-1\right)^2\cdot\left(x^2-2x\right)\) với \(\forall x\in R\). Có bao nhiêu giá trị nguyên dương của tham số m để hàm...

Đọc tiếp

#Toán lớp 12

1

SV

Sinh Viên NEU

CTVVIP

11 tháng 11 2023

48 D

50 loading...

loading...

Đúng(1)

SV

Sinh Viên NEU

CTVVIP

11 tháng 11 2023

xem có j k hiểu hỏi a nha

Đúng(1)

QT

Quoc Tran Anh Le

Giáo viên

24 tháng 9 2023

Biết rằng hàm số \(y = 2{x^2}{\rm{ + }}mx + n\) giảm trên khoảng \(\left( { - \infty ;1} \right),\)tăng trên khoảng \(\left( {1; + \infty } \right)\) và có tập giá trị là \([9; + \infty )\). Xác định giá trị của m và n.

#Toán lớp 10

1

KS

Kiều Sơn Tùng

24 tháng 9 2023

Tham khảo:

Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - m}}{{2.2}} = - \frac{m}{4};{y_S} = f( - \frac{m}{4})\)

Vì hàm số bậc hai có \(a = 2 > 0\) nên ta có bảng biến thiên sau:

Hàm số đạt giá trị nhỏ nhất bằng \(f( - \frac{m}{4}).\)

Hàm số giảm trên \(( - \infty ; - \frac{m}{4})\) và tăng trên \(( - \frac{m}{4}; + \infty )\)

Theo giả thiết, ta có:

Hàm số giảm trên khoảng \(\left( { - \infty ;1} \right)\)\( \Rightarrow \left( { - \infty ;1} \right) \subset ( - \infty ; - \frac{m}{4}) \Leftrightarrow 1 \le - \frac{m}{4}.\)

Tương tự hàm số tăng trên khoảng \(\left( {1; + \infty } \right)\)\( \Rightarrow \left( {1; + \infty } \right) \subset ( - \frac{m}{4}; + \infty ) \Leftrightarrow - \frac{m}{4} \le 1.\)

Do đó: \( - \frac{m}{4} = 1\) hay \(m = - 4\)

Lại có: Tập giá trị là \([9; + \infty )\)\( \Rightarrow \)Giá trị nhỏ nhất của hàm số bằng 9.

\( \Leftrightarrow f(1) = f( - \frac{m}{4}) = 9 \Leftrightarrow {2.1^2} + ( - 4).1 + n = 9 \Leftrightarrow n = 11.\)

Vậy \(m = - 4,n = 11.\)

Đúng(0)

LP

lê phương thảo

11 tháng 8 2021

xét tính đồng biến nghịch biến của các hàm số trên

\(y=f\left(x\right)=x^2-2x+3\) trên khoảng \(_{\left(1;+\infty\right)}\)

y=f(x)=\(\sqrt{3-x}\) trên khoảng \(\left(-\infty;3\right)\)

#Toán lớp 10

0

MA

Mai Anh

14 tháng 4 2022

Cho hàm số y=f(x) xác định trên (a;b). Nếu \(\forall\left(x_o\right),x_n\ne x_o,l\text{imx}_n=x_o\Rightarrow...

Đọc tiếp

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

14 tháng 4 2022

\(\lim\limits_{x\rightarrow x_0}f\left(x\right)=+\infty\)

Đúng(0)

C

Crackinh

11 tháng 3 2022

Cho hàm số y = f(x) có đạo hàm cấp hai trên \(\left(0;+\infty\right)\) thỏa mãn: \(2xf'\left(x\right)-f\left(x\right)=x^2\sqrt{x}cosx,\forall x\in\left(0;+\infty\right)\) và \(f\left(4\Pi\right)=0\)

Tính giá trị biểu thức \(f\left(9\Pi\right)\)

#Toán lớp 12

1

NV

Nguyễn Việt Lâm

Giáo viên

11 tháng 3 2022

\(2x.f'\left(x\right)-f\left(x\right)=x^2\sqrt{x}.cosx\)

\(\Leftrightarrow\dfrac{1}{\sqrt{x}}.f'\left(x\right)-\dfrac{1}{2x\sqrt{x}}f\left(x\right)=x.cosx\)

\(\Leftrightarrow\left[\dfrac{f\left(x\right)}{\sqrt{x}}\right]'=x.cosx\)

Lấy nguyên hàm 2 vế:

\(\int\left[\dfrac{f\left(x\right)}{\sqrt{x}}\right]'dx=\int x.cosxdx\)

\(\Rightarrow\dfrac{f\left(x\right)}{\sqrt{x}}=x.sinx+cosx+C\)

\(\Rightarrow f\left(x\right)=x\sqrt{x}.sinx+\sqrt{x}.cosx+C.\sqrt{x}\)

Thay \(x=4\pi\)

\(\Rightarrow0=4\pi.\sqrt{4\pi}.sin\left(4\pi\right)+\sqrt{4\pi}.cos\left(4\pi\right)+C.\sqrt{4\pi}\)

\(\Rightarrow C=-1\)

\(\Rightarrow f\left(x\right)=x\sqrt{x}.sinx+\sqrt{x}.cosx-\sqrt{x}\)

Đúng(1)

QT

Quoc Tran Anh Le

Giáo viên

30 tháng 9 2023

Cho hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\)a) Xác định hệ số a. Tính \(f(0);f(1);f(2);f(3);f(4)\) và nhận xét về dấu của chúng so với dấu của hệ số ab) Cho đồ thị hàm số y=f(x) (H.6.17). Xét từng khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\), đồ thị nằm phía trên hay phía dưới trục Ox?c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng...

Đọc tiếp

#Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

30 tháng 9 2023

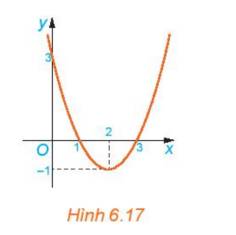
a) Hệ số a là: a=1

\(f(0) = {0^2} - 4.0 + 3 = 3\)

\(f(1) = {1^2} - 4.1 + 3 = 0\)

\(f(2) = {2^2} - 4.2 + 3 = - 1\)

\(f(3) = {3^2} - 4.3 + 3 = 0\)

\(f(4) = {4^2} - 4.4 + 3 = 3\)

=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a

b) Nhìn vào đồ thị ta thấy

- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành

- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành

- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành

c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a

- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a

- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a

Đúng(0)

SG

Sách Giáo Khoa

10 tháng 4 2017

Cho hàm số \(y=f\left(x\right)\) xác định trên khoảng \(\left(a;+\infty\right)\)

Chứng minh rằng nếu \(\lim\limits_{x\rightarrow+\infty}=-\infty\) thì luôn tồn tại ít nhất một số c thuộc \(\left(a;+\infty\right)\) sao cho \(f\left(c\right)< 0\)

#Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 5 2022

Tham khảo:

Đúng(0)

SG

Sách Giáo Khoa

11 tháng 4 2017

Xác định một hàm số \(y=f\left(x\right)\) thỏa mãn đồng thời các điều kiện sau :

a) \(f\left(x\right)\) xác định trên R\{1}

b) \(\lim\limits_{x\rightarrow1}f\left(x\right)=+\infty;\lim\limits_{x\rightarrow+\infty}f\left(x\right)=2;\lim\limits_{x\rightarrow-\infty}f\left(x\right)=2\)

#Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 5 2022

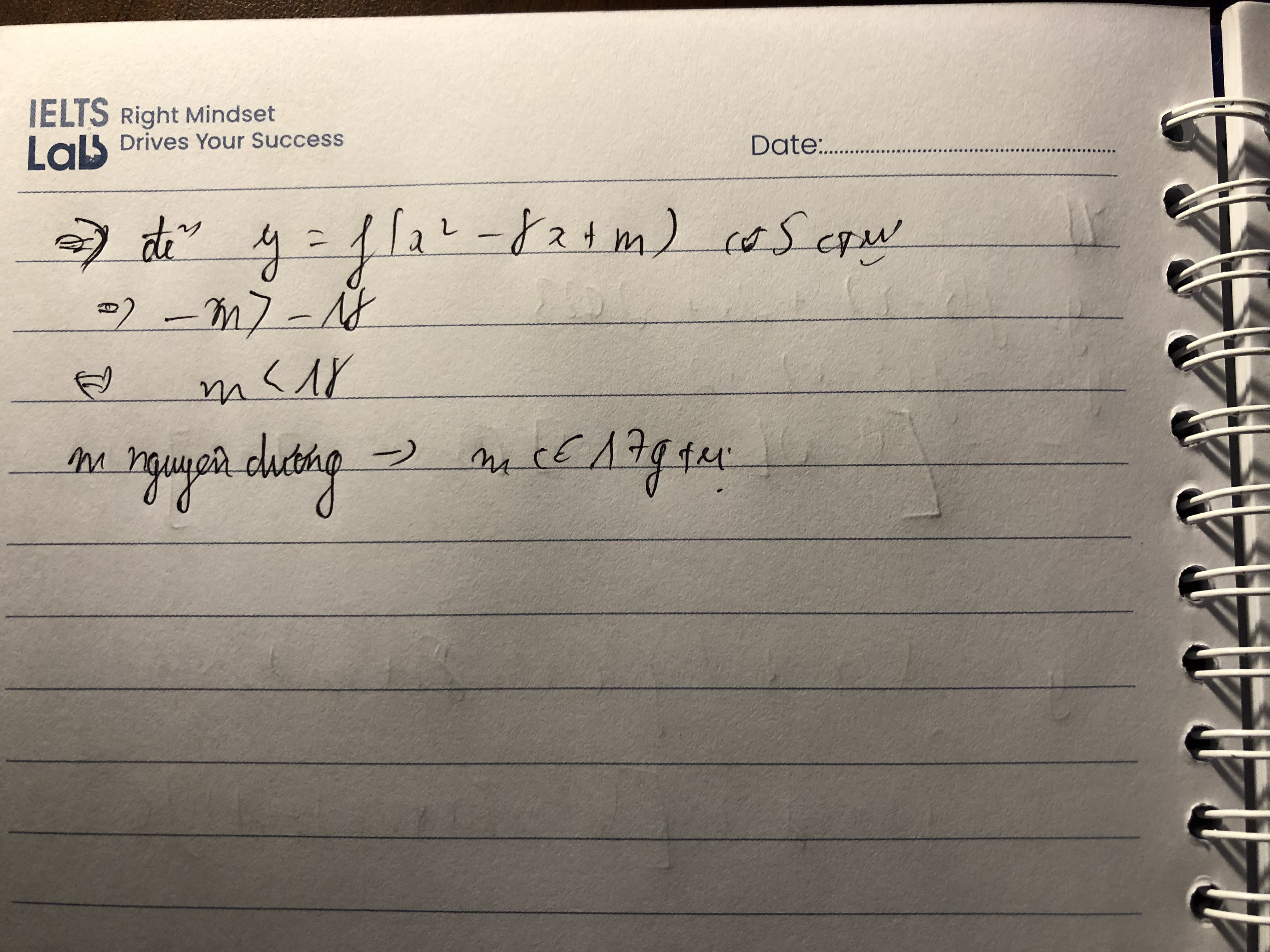
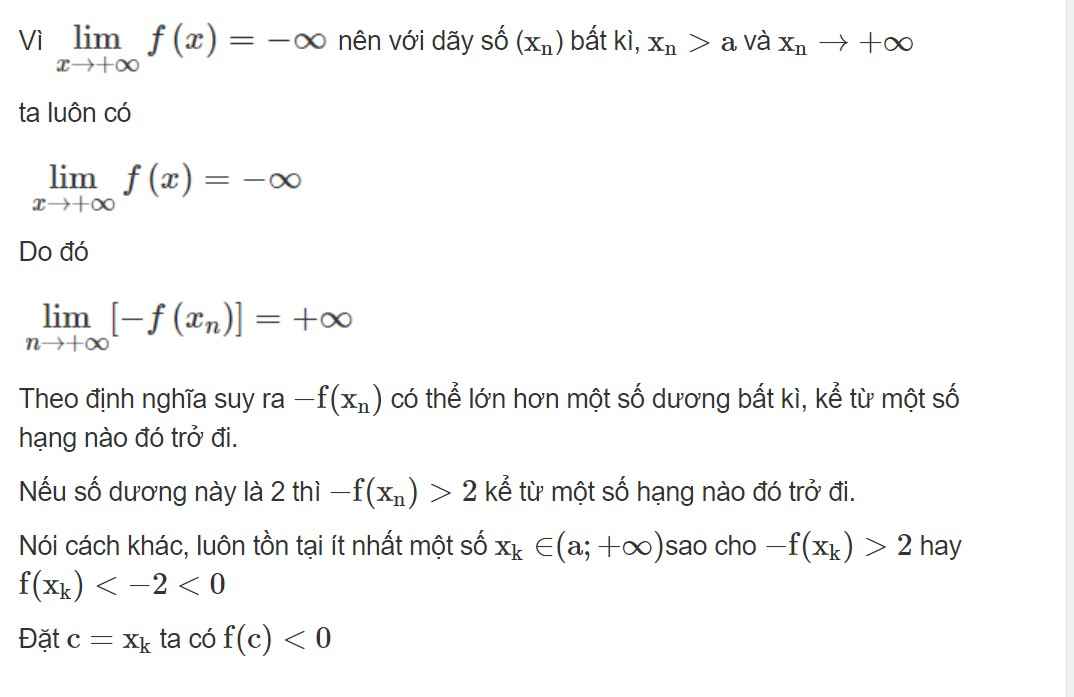
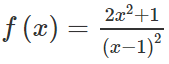Giải sách bài tập Toán 11 | Giải sbt Toán 11 thì f(x) thỏa mãn được tất cả các điều kiện đã nêu

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP