Gọi f là 1 hàm xác định trên tập hợp các số nguyên và thoả mãn các điều kiện sau f(0) khác 0, f(1)=3, f(x) . f(y) = f( x + y ) + f ( x- y ) với mọi x,y thuộc Z. tính giá trị của f (7)
HELP... HELP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
1 tháng 4 2018
theo đề ra ta có f(1)f(0)=f(1+0)+f(1-0) \(\Rightarrow\)3f(0)=3+3\(\Rightarrow\)f(0)=2
f(2)f(0)=f(2+0)+f(2-0) \(\Rightarrow\)2f(2)=2+2\(\Rightarrow\)f(2)=2
f(2)f(1)=f(2+1)+f(2-1) \(\Rightarrow\)2.3=f(3)+3\(\Rightarrow\)f(3)=3
f(3)f(2)=f(3+2)+f(3-2) \(\Rightarrow\)2.3=f(5)+3\(\Rightarrow\)f(5)=3
f(5)f(2)=f(5+2)+f(5-2) \(\Rightarrow\)2.3=f(7)+3\(\Rightarrow\)f(7)=3
CM
22 tháng 9 2018
Đáp án C
Ta có f ' x = - e x . f 2 x ⇔ f ' x f 2 x = - e x ⇔ ∫ f ' x f 2 x d x = ∫ - e x d x = ∫ d f x f 2 x d x = - e x + C
⇔ - 1 f x = - e x + C ⇔ f x = 1 e x - C mà f 0 = 1 2 ⇒ 1 1 - C = 1 2 ⇒ C = - 1
Vậy f x = 1 e x + 1 ⇒ f ln 2 = 1 e ln 2 + 1 = 1 2 + 1 = 1 3 .
CM
10 tháng 10 2017
Chẳng hạn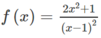 
.
Dễ dàng kiểm tra được rằng f(x) thoả mãn các điều kiện đã nêu
CM
18 tháng 1 2018
Chọn C.
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)
Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.