Cho tình hình ABCD có AB = 3a; AD = 5a. Góc BAD bằng \(120^0\) :
a) Tìm các tích vô hướng sau : \(\overrightarrow{AB}.\overrightarrow{AD};\overrightarrow{AC}.\overrightarrow{BD}\)
b) Tính độ dài BD và bán kính đường tròn ngoại tiếp tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



S A B C D H E K F
Ta có
\(SH\perp\left(ABCD\right);SH\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(ABCD\right)\)
Trong mp (ABCD) từ C dựng đường thẳng vuông góc với BD cắt BD tại F ta có
\(SH\perp\left(ABCD\right);CF\in ABCD\Rightarrow SH\perp CF\)
Mà \(CF\perp BD\)
Ta có \(BD\in\left(SBD\right);SH\in\left(SBD\right)\)
\(\Rightarrow CF\perp\left(SBD\right)\) => CF là khoảng cách từ C đến (SBD)
Trong mp (ABCD) nối CH cắt AD tại E
Ta có BC//AD \(\Rightarrow\dfrac{BC}{ED}=\dfrac{HB}{HD}=\dfrac{HC}{HE}=1\Rightarrow ED=BC=\dfrac{3a}{2}\)
\(\Rightarrow EA=AD-ED=3a-\dfrac{3a}{2}=\dfrac{3a}{2}=BC\)
Mà BC//AE và \(\widehat{ABC}=90^o\)
=> ABCE là hình chữ nhật
Trong mp (ABCD) từ H dựng đường thẳng vuông góc với CD cắt CD tại K
Xét tg vuông CDE có
\(CD=\sqrt{CE^2+ED^2}=\sqrt{4a^2+\dfrac{9a^2}{4}}=\dfrac{5a}{2}\)
Xét tg vuông ABD có
\(BD=\sqrt{AB^2+AD^2}=\sqrt{4a^2+9a^2}=a\sqrt{13}\)
\(\Rightarrow HB=HD=\dfrac{BD}{2}=\dfrac{a\sqrt{13}}{2}\)
Xét tg vuông CKH và tg vuông CED có \(\widehat{ECD}\) chung
=> tg CKH đồng dạng với tg CED (g.g.g)
\(\Rightarrow\dfrac{CK}{CE}=\dfrac{HC}{CD}\Rightarrow CK=\dfrac{CE.HC}{CD}=\dfrac{2a.a}{\dfrac{5a}{2}}=\dfrac{4a}{5}\)
Xét tg vuông CKH có
\(HK=\sqrt{HC^2-CK^2}=\sqrt{a^2-\dfrac{16a^2}{25}}=\dfrac{3a}{5}\)
Xét tg vuông DKH và tg vuông DFC có \(\widehat{BDC}\) chung
=> tg DKH đồng dạng với tg DFC (g.g.g)
\(\Rightarrow\dfrac{HK}{CF}=\dfrac{HD}{CD}\Rightarrow CF=\dfrac{HK.CD}{HD}=\dfrac{\dfrac{3a}{5}.\dfrac{5a}{2}}{\dfrac{a\sqrt{13}}{2}}=\dfrac{3a\sqrt{13}}{13}\)

\(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=AC=5a\)

Đáp án là B
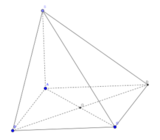
Tam giác ABC vuông tại B nên
![]()
Tam giác SAC vuông tại A nên
![]()
Thể tích hình chóp S.ABCD là
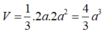

(SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=3/2
=>góc SDA=56 độ

Đáp án B
Thể tích khối chóp S.ABCD là:
V A B C D = 1 3 S A . S A B C D = 1 3 2 a .3 a 2 = 2 a 3