Cho lục giác đều ABCDEF tâm O có cạnh a
a) Phân tích vectơ \(\overrightarrow{AD}\) theo hai vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{AF}\)
b) Tính độ dài của vectơ \(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}\) theo a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BT
16 tháng 5 2017
Do các tam giác OAB, OCD, OED, OEF, OFA , OBC cùng là tam giác đều nên OA = OB = OC = OD = OE = OF = 6cm.
Do \(\overrightarrow{i}\) và \(\overrightarrow{OD}\) cùng hướng nên D(6;0), A (0;-6).
Áp dụng hệ thức lượng trong tam giác vuông ta được:\(EC=2.DC.sin60^o=2.6.\dfrac{\sqrt{3}}{2}=6\sqrt{3}\).
\(\overrightarrow{EC}\) cùng hướng với \(\overrightarrow{j}\) nên:
Suy ra \(y_B=y_C=3\sqrt{3}\); \(y_E=y_F=-3\sqrt{3}\).
Do BC = 6cm và BC // OD nên \(x_E=x_C=3;x_F=x_B=-3\).
Vậy \(A\left(-6;0\right);D\left(6;0\right);B\left(-3;3\sqrt{3}\right),C\left(3;3\sqrt{3}\right)\);\(E\left(3;-3\sqrt{3}\right)\)\(F\left(-3;-3\sqrt{3}\right)\) .
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
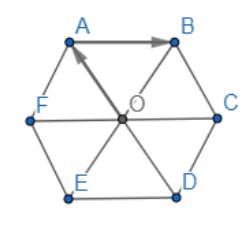
a) Ta có: AO // BC // EF
Suy ra các vectơ khác vectơ khác vectơ \(\overrightarrow 0 \) và cùng hướng với vectơ \(\overrightarrow {OA} \) là : \(\overrightarrow {DO} ,\overrightarrow {DA} ,\overrightarrow {CB} ,\overrightarrow {EF} \)
b) Ta có: \(OA = OB = OC = OD = OE = FO\) và AB // FC // ED
Suy ra các vectơ bằng vectơ \(\overrightarrow {AB} \) là \(\overrightarrow {FO} ,\overrightarrow {OC} ,\overrightarrow {ED} \)
24 tháng 9 2023
Tham khảo:
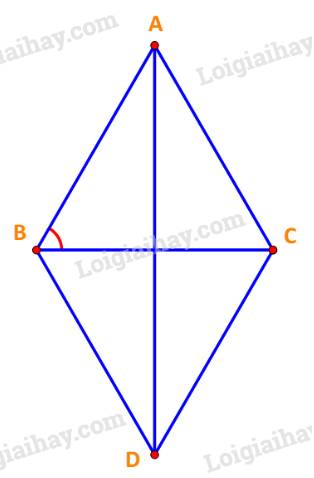
\(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = CB = a.\)
Dựng hình bình hành ABDC tâm O như hình vẽ.
Ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
\( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Vì tứ giác ABDC là hình bình hành, lại có \(AB = AC = BD = CD = a\) nên ABDC là hình thoi.
\( \Rightarrow AD = 2AO = 2.AB.\sin B = 2a.\frac{{\sqrt 3 }}{2} = a\sqrt 3 .\)
Vậy \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = a\) và \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \).
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Dựng hình bình hành ABDC.
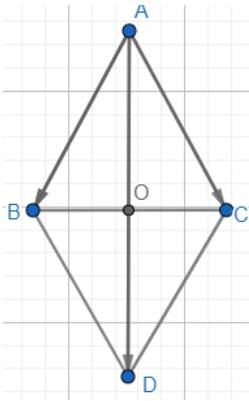
Áp dụng quy tắc hình bình hành vào ABDC ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Gọi O là giao điểm của AD và BC, ta có:
\(AO = \sqrt {A{B^2} - B{O^2}} = \sqrt {A{B^2} - {{\left( {\frac{1}{2}BC} \right)}^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(AD = 2AO = a\sqrt 3 \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \)
Vậy độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) là \(a\sqrt 3 \)
BT
18 tháng 5 2017
Các véc tơ bằng véc tơ \(\overrightarrow{AB}\) là:
\(\overrightarrow{OC};\overrightarrow{FO};\overrightarrow{ED}\).
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Ta có: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
\( \Leftrightarrow 12\sqrt 2 = 3.8.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) \Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\sqrt 2 }}{2}\)
\( \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 45^\circ \)
Vậy góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là \(45^\circ \)
a)
\(\overrightarrow{AO}=\overrightarrow{AB}+\overrightarrow{BO}=\overrightarrow{AB}+\overrightarrow{AF}\).
Vậy \(\overrightarrow{AD}=2\overrightarrow{AO}=2\left(\overrightarrow{AB}+\overrightarrow{AF}\right)\).
b)
\(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)=\dfrac{1}{2}\overrightarrow{AC}\).
Vì vậy: \(\left|\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}\right|=\left|\dfrac{1}{2}\overrightarrow{AC}\right|=\dfrac{1}{2}AC\).
Do tam giác ABC cân tại B nên BH là đường cao, đường trung tuyến, đường phân giác ứng với đỉnh B của tam giác ABC.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(AH=AB.sin60^o=\dfrac{a\sqrt{3}}{2}\).
\(AC=2BH=2.\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\).
Vì vậy: \(\left|\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}\right|=\left|\dfrac{1}{2}\overrightarrow{AC}\right|=\dfrac{1}{2}AC\)\(=a\sqrt{3}\).