Cho phương trình \(7x^2+2\left(m-1\right)x-m^2=0.\)
a) Với giá trị nào của m thì phương trình có nghiệm?
b) Trong trường hợp phương trình có nghiệm, dùng hệ thức Vi-et, hãy tính tổng các bình phương hai nghiệm của phương trình đã cho theo m.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 4 2016
phương trình có a = 7 khác 0 => là phương trình bậc 2
vậy phương trình có nghiệm <=> \(\Delta'\ge0\Leftrightarrow\left(m-1\right)^2-7.\left(-m^2\right)\ge0\Leftrightarrow\left(m-1\right)^2+7m^2\ge0\)(thỏa mãn với mọi m)
b) theo vi et ta có
+) x1+x2 = -b/a = 2(m-1)/7
+) x1.x2 = c/a = -m2/7
HH
22 tháng 1 2021
a) Ta có : a = 7 ; b = 2(m-1) ; c = -m2
\(\Rightarrow\Delta'=\left(m-1\right)^2+7m^2\)
Do \(\left(m-1\right)^2\ge0\)mọi m và \(m^2\ge0\)mọi m
\(\Rightarrow\Delta'\ge0\)với mọi giá trị của m
Do đó PT có nghiệm với mọi giá trị của m
b) Gọi 2 nghiệm của PT là x1 ; x2
Theo định lí Vi-ét , ta có : \(\hept{\begin{cases}x_1+x_2=\frac{-2\left(m-1\right)}{7}\\x_1.x_2=\frac{-m^2}{7}\end{cases}}\)
Khi đó : \(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2.x_1.x_2\)
\(=\left[\frac{-2\left(m-1\right)}{7}\right]^2-2.\frac{-m^2}{7}\)
\(=\frac{4\left(m-1\right)^2}{49}+\frac{2m^2}{7}\)
\(=\frac{4m^2-8m+4+14m^2}{49}\)
\(=\frac{18m^2-8m+4}{49}\)
CM
16 tháng 1 2017
a) Ta có: a = 7, b= 2(m-1), c = - m 2
Suy ra: Δ ' = ( m - 1 ) 2 + 7 m 2
Do ( m - 1 ) 2 ≥ 0 mọi m và m 2 ≥ 0 mọi m
=> ∆’≥ 0 với mọi giá trị của m.
Do đó phương trình có nghiệm với mọi giá trị của m.
b) Gọi hai nghiệm của phương trình là x 1 ; x 2 .
Theo định lý Vi-et ta có: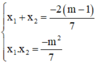 
Khi đó:
CM
28 tháng 8 2018
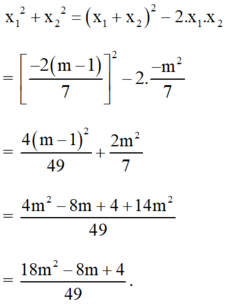
Gọi hai nghiệm của phương trình là x1; x2.
Theo định lý Vi-et ta có: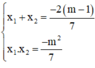 
Khi đó:
Y
1 tháng 4 2023
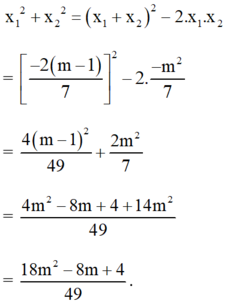
\(x^2+2\left(2m-1\right)x+3\left(m^2-1\right)=0\)
\(a,\) Để pt có nghiệm thì \(\Delta\ge0\)
\(\Rightarrow\left[2\left(2m-1\right)\right]^2-4\left[3\left(m^2-1\right)\right]\ge0\)
\(\Rightarrow4\left(4m^2-4m+1\right)-4\left(3m^2-3\right)\ge0\)
\(\Rightarrow16m^2-16m+4-12m^2+12\ge0\)
\(\Rightarrow4m^2-16m+16\ge0\)
\(\Rightarrow\left(2m-4\right)^2\ge0\)
Vậy pt có nghiệm với mọi m.
LD
1 tháng 4 2023
b, Theo viét : \(\left\{{}\begin{matrix}x_1+x_2=-2\left(2m-1\right)\\x_1x_2=3\left(m^2-1\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=-4m+2\\x_1x_2=3m^2-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{-2+x_1+x_2}{4}\\x_1x_2=3\left(\dfrac{-2+x_1+x_2}{4}\right)^2-3\end{matrix}\right.\)
Vậy......
2
13 tháng 1 2023
`1)` Ptr có: `\Delta=3^2-4.5.(-1)=29 > 0 =>`Ptr có `2` nghiệm phân biệt
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=-3/5),(x_1.x_2=c/a=-1/5):}`
Có: `A=(3x_1+2x_2)(3x_2+x_1)`
`A=9x_1x_2+3x_1 ^2+6x_2 ^2+2x_1x_2`
`A=8x_1x_2+3(x_1+x_2)^2=8.(-1/5)+3.(-3/5)^2=-13/25`
Vậy `A=-13/25`
____________________________________________________
`2)` Ptr có: `\Delta'=(-1)^2-7.(-3)=22 > 0=>` Ptr có `2` nghiệm pb
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=2/7),(x_1.x_2=c/a=-3/7):}`
Có: `M=[7x_1 ^2-2x_1]/3+3/[7x_2 ^2-2x_2]`
`M=[(7x_1 ^2-2x_1)(7x_2 ^2-2x_2)+9]/[3(7x_2 ^2-2x_2)]`
`M=[49(x_1x_2)^2-14x_1 ^2 x_2-14x_1 x_2 ^2+4x_1x_2+9]/[3(7x_2 ^2-2x_2)]`
`M=[49.(-3/7)^2-14.(-3/7)(2/7)+4.(-3/7)+9]/[3x_2(7x_2-2)]`
`M=6/[x_2(7x_2-2)]` `(1)`
Có: `x_1+x_2=2/7=>x_1=2/7-x_2`
Thay vào `x_1.x_2=-3/7 =>(2/7-x_2)x_2=-3/7`
`<=>-x_2 ^2+2/7 x_2+3/7=0<=>x_2=[1+-\sqrt{22}]/7`
`@x_2=[1+\sqrt{22}]/7=>M=6/[[1+\sqrt{22}]/7(7 .[1+\sqrt{22}]/2-2)]=2`
`@x_2=[1-\sqrt{22}]/7=>M=6/[[1-\sqrt{22}]/7(7 .[1-\sqrt{22}]/2-2)]=2`
Vậy `M=2`
CM
11 tháng 11 2018
a) Xét: x2 - 4mx + 9.(m – 1)2 = 0 (1)
Δ’ = (2.m)2 – 9.(m – 1)2 = 4m2 – 9.(m2 – 2m + 1) = -5m2 + 18m – 9
Phương trình (1) có nghiệm ⇔ Δ’ ≥ 0
⇔ -5m2 + 18m – 9 ≥ 0
⇔ 5m2 - 18m + 9 ≤ 0
⇔ (5m – 3)(m – 3) ≤ 0
⇔ 3/5 ≤ m ≤ 3.
b) + x1 ; x2 là hai nghiệm của (1) nên theo định lý Vi-et ta có:
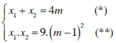
+ Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.
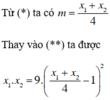
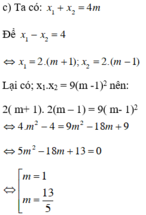
Thử lại:
+ m = 1, (1) trở thành x2 – 4x = 0 có hai nghiệm x = 0; x = 4 có hiệu bằng 4
+ m = 13/5, (1) trở thành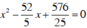 
có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
Vậy m = 1 hoặc m = 13/5.
CM
24 tháng 8 2018
Theo hệ thức Vi-ét ta có: x 1 x 2 =5/3
Suy ra: 1/3 . x 2 = 5/3 ⇔ x 2 =5/3 : 1/3 =5/3 .3=5
cũng theo hệ thức Vi-ét ta có: x 1 + x 2 =[2(m -3)]/3
Suy ra: 1/3 +5 = [2(m -3)]/3 ⇔ 2(m -3) =16 ⇔ m-3=8 ⇔ m=11
Vậy với m = 11 thì phương trình 3 x 2 -2(m -3)x +5 =0 có hai nghiệm x 1 = 1/3 , x 2 = 5
4 tháng 2 2022
a: Ta có: \(\left(m-1\right)x^2-2x-m+1=0\)
a=m-1; b=-2; c=-m+1
\(ac=\left(m-1\right)\left(-m+1\right)=-\left(m-1\right)^2< 0\forall m\)
Do đó: Phương trình luôn có hai nghiệm trái dấu
b: \(x_1^2+x_2^2=6\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\)
\(\Leftrightarrow\left(\dfrac{2}{m-1}\right)^2-2\cdot\dfrac{-m+1}{m-1}=6\)
\(\Leftrightarrow\dfrac{4}{\left(m-1\right)^2}=4\)
\(\Leftrightarrow\left(m-1\right)^2=1\)
=>m-1=1 hoặc m-1=-1
=>m=2 hoặc m=0
Xét phương trình 7x2 + 2(m – 1)x – m2 = 0 (1)
a) Phương trình có nghiệm khi ∆’ ≥ 0
Ta có: ∆’ = (m – 1)2 – 7(-m2) = (m – 1)2 + 7m2 ≥ 0 với mọi m
Vậy phương trình (1) luôn luôn có nghiệm với mọi giá trị của m
b) Gọi x1, x2 là hai nghiệm của phương trình (1)
Ta có:
\(x^2_1+x^2_2=\left(x_1+x_2\right)^2-2x_1x_2\\ =\left[\dfrac{-2\left(m-1\right)^2}{7}\right]-2\dfrac{\left(-m\right)^2}{7}\\ =\dfrac{4m^2-8m+4}{49}+\dfrac{2m^2}{7}\\ =\dfrac{4m^2-8m+4+14m^2}{49}\\ =\dfrac{18m^2-8m+4}{49}\)
Vậy \(x^2_1+x^2_2=\dfrac{18m^2-8m+4}{49}\).
Xét phương trình 7x2 + 2(m – 1)x – m2 = 0 (1)
a) Phương trình có nghiệm khi ∆’ ≥ 0
Ta có: ∆’ = (m – 1)2 – 7(-m2) = (m – 1)2 + 7m2 ≥ 0 với mọi m
Vậy phương trình (1) luôn luôn có nghiệm với mọi giá trị của m
b) Gọi x1, x2 là hai nghiệm của phương trình (1)
Ta có:
x\(\dfrac{1}{2}\)+x\(\dfrac{2}{2}\)=(x1+x2)2−2x1x2
=[\(\dfrac{-2\left(m-1\right)^2}{7}\)]-2\(\dfrac{\left(-m\right)^2}{7}\)
=\(\dfrac{4m^2-8m+4}{49}\)+\(\dfrac{2m^2}{7}\)
=\(\dfrac{4m^2-8m+4+14m^2}{49}\)
=\(\dfrac{18m^2-8m+4}{49}\)
vậy x\(\dfrac{2}{1}\)+x\(\dfrac{2}{2}\)=\(\dfrac{18m^2-8m+4}{49}\)