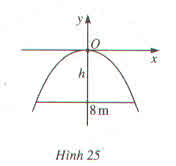
Một chiếc cổng hình parabl dạng \(y=-\dfrac{1}{2}x^2\) có chiều rộng \(d=8m\). Hãy tính chiều cao h của cổng (h.25) ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do tính đối xứng của parabol, \(\Rightarrow H\) là trung điểm AB \(\Rightarrow y_H=y_A=y_B\) đồng thời \(x_A=-x_B\)
Mặt khác \(AB=\left|x_A-x_B\right|=\left|2x_A\right|=4\Rightarrow x_A=2\)
\(\Rightarrow y_A=-x_A^2=-4\Rightarrow y_H=-4\)
\(\Rightarrow OH=\left|y_H\right|=4\) (m)

Lời giải:
a) Chiều dài khu vườn là:
$23\frac{1}{4}+7\frac{1}{2}=\frac{123}{4}$ (m)
b)
Nếu bạn muốn tính diện tích khu vườn (mà không gồm phần cổng) thì đề còn thiếu dữ kiện chiều dài cổng.
Lời giải
Parabol nhận trục tung là trục đối xứng
(điểm thấp nhất thuộc đồ thị có tọa độ A(4,ya)
\(y\left(4\right)=-\dfrac{1}{2}.4^2=-8\)
Vậy chiều cao cổng là 8m