Tính A= 1-5+52-53+54-55+.....+598-599
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 11 2023
Đề bài thiếu yêu cầu cụ thể em nhé. em cập nhật lại câu hỏi để được sự hỗ trợ tốt nhất cho tài khoản olm vip
NM
4
BD
29 tháng 6 2023
0\(a.S=1-5+5^2-5^3+...+5^{98}-5^{99}\\ 5S=5-5^2+5^3-5^4+.....+5^{99}-5^{100}\\ 5S+S=\left(5-5^2+5^3-5^4+.....+5^{99}-5^{100}\right)+\left(1-5^{ }+5^2-5^3+.....+5^{98}-5^{99}\right)\\ 6S=1-5^{100}\\ S=\dfrac{1-5^{100}}{6}\\ \)
\(b,S6=1-5^{100}\\ 1-S6=5^{100}\)
=> 5100 chia 6 du 1
2 tháng 11 2021
Bài 1:
1) \(9A=3^3+3^5+...+3^{113}\)
\(\Rightarrow8A=9A-A=3^3+3^5+...+3^{113}-3-3^3-...-3^{111}=3^{113}-3\)
\(\Rightarrow A=\dfrac{3^{113}-3}{8}\)
2) \(9B=3^4+3^6+...+3^{202}\)
\(\Rightarrow8B=9B-B=3^4+3^6+...+3^{202}-3^2-3^4-...-3^{200}=3^{202}-3^2=3^{202}-9\)
\(\Rightarrow B=\dfrac{3^{202}-9}{8}\)
3) \(25C=5^3+5^5+...+5^{101}\)
\(\Rightarrow24C=25C-C=5^3+5^5+...+5^{101}-5-5^3-...-5^{99}=5^{101}-5\)
\(\Rightarrow C=\dfrac{5^{101}-5}{24}\)
4) \(25D=5^4+5^6+...+5^{102}\)
\(\Rightarrow24D=25D-D=5^4+5^6+...+5^{102}-5^2-5^4-...-5^{100}=5^{102}-25\)
\(\Rightarrow D=\dfrac{5^{102}-25}{24}\)
2 tháng 11 2021
Bài 2:
a) Gọi d là UCLN(2n+1,n+1)
\(\Rightarrow\left\{{}\begin{matrix}2n+1⋮d\\n+1⋮d\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}2n+1⋮d\\2n+2⋮d\end{matrix}\right.\)
\(\Rightarrow\left(2n+2\right)-\left(2n+1\right)⋮d\Rightarrow1⋮d\)
Vậy 2n+1 và n+1 là 2 số nguyên tố cùng nhau
\(\Rightarrow\dfrac{2n+1}{n+1}\) là phân số tối giản
b) Gọi d là UCLN(2n+3,3n+4)
\(\Rightarrow\left\{{}\begin{matrix}2n+3⋮d\\3n+4⋮d\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}6n+9⋮d\\6n+8⋮d\end{matrix}\right.\)
\(\Rightarrow\left(6n+9\right)-\left(6n+8\right)⋮d\Rightarrow1⋮d\)
\(\Rightarrow\dfrac{2n+3}{3n+4}\) là phân số tối giản
CM
20 tháng 2 2019
a, Ta có :
A = 1 + 2 + 2 2 + 2 3 + 2 4 + . . . + 2 99 + 2 100
2A = 2 + 2 2 + 2 3 + 2 4 + . . . + 2 99 + 2 100 + 2 101
A = 2A – A = ( 2 + 2 2 + 2 3 + 2 4 + . . . + 2 99 + 2 100 + 2 101 ) –( 1 + 2 + 2 2 + 2 3 + 2 4 + . . . + 2 99 + 2 100 )
= 2 + 2 2 + 2 3 + 2 4 + . . . + 2 99 + 2 100 + 2 101 – 1 - 2 - 2 2 - 2 3 - 2 4 - . . . - 2 99 - 2 100
= 2 101 - 1
Vậy A = 2 101 - 1
b, Ta có.
B = 5 + 5 3 + 5 5 + . . . + 5 97 + 5 99
5 2 B = 5 2 ( 5 + 5 3 + 5 5 + . . . + 5 97 + 5 99 )
25B = 5 3 + 5 5 + . . . + 5 97 + 5 99 + 5 101
25B – B = ( 5 3 + 5 5 + . . . + 5 97 + 5 99 + 5 101 ) – ( 5 + 5 3 + 5 5 + . . . + 5 97 + 5 99 )
24B = 5 3 + 5 5 + . . . + 5 97 + 5 99 + 5 101 – 5 - 5 3 - 5 5 - . . . - 5 97 - 5 99
24B = 5 101 - 5
B = 5 101 - 5 24 = 5 5 100 - 1 24
Vậy B = 5 5 100 - 1 24
KJ
6
PD
1
29 tháng 11 2023
Bài 1:
a: \(S=1-5+5^2-5^3+...+5^{98}-5^{99}\)
=>\(5S=5-5^2+5^3-5^4+...+5^{99}-5^{100}\)
=>\(6S=5-5^2+5^3-5^4+...+5^{99}-5^{100}+1-5+5^2-5^3+...+5^{98}-5^{99}\)
=>\(6S=-5^{100}+1\)
=>\(S=\dfrac{-5^{100}+1}{6}\)
b: S=1-5+52-53+...+598-599 là số nguyên
=>\(\dfrac{-5^{100}+1}{6}\in Z\)
=>\(-5^{100}+1⋮6\)
=>\(5^{100}-1⋮6\)
=>\(5^{100}\) chia 6 dư 1
NH
4
KV
15 tháng 10 2023
S = 5 + 5² + 5³ + 5⁴ + ... + 5²⁰¹²
= (5 + 5² + 5³ + 5⁴) + (5⁵ + 5⁶ + 5⁷ + 5⁸) + ... + (5²⁰⁰⁹ + 5²⁰¹⁰ + 5²⁰¹¹ + 5²⁰¹²)
= 780 + 5⁴.(5 + 5² + 5³ + 5⁴) + ... + 5²⁰⁰⁸.(5 + 5² + 5³ + 5⁴)
= 780 + 5⁴.780 + ... + 5²⁰⁰⁸.780
= 65.12 + 5⁴.65.12 + ... + 5²⁰⁰⁸.65.12
= 65.12(1 + 5⁴ + ... + 5²⁰⁰⁸) ⋮ 65
Vậy S ⋮ 65
CM
4 tháng 1 2020
a, A = 1 + 5 3 + 5 5 + 5 7 + . . . + 5 99
B = 5 4 + 5 6 + 5 8 + . . . + 5 100 = 5 . ( 5 3 + 5 5 + 5 7 + . . . + 5 99 ) = 5(A – 1)
A + B – 1 = 5 3 + 5 4 + . . . + 5 100
5(A + B – 1) = 5 4 + 5 5 + . . . + 5 100 + 5 101
4(A + B – 1) = 5(A + B – 1) – (A + B – 1) = 5 101 - 5 3
=> A + B – 1 = 5 101 - 5 3 4
=> A + 5(A – 1) –1 = 5 101 - 5 3 4 => 6A – 6 = 5 101 - 5 3 4
=> A – 1 = 5 101 - 5 3 24
=> A = 5 101 - 5 3 + 24 24
b, A = 1 - 2 + 2 2 - . . . - 2 2007
A = 1 + 2 2 + . . . + 2 2006 - 2 + 2 3 + . . . + 2 2007
A = ( 1 + 2 2 + . . . + 2 2006 ) - 2 . 1 + 2 2 + . . . + 2 2006
A = - 1 + 2 2 + . . . + 2 2006
Đặt B = - 2 + 2 3 + . . . + 2 2007 = - 2 . 1 + 2 2 + . . . + 2 2006 = 2A
A + B = - 1 + 2 + 2 2 + . . . + 2 2006 + 2 2007
2(A+B) = - 2 + 2 2 + . . . + 2 2006 + 2 2007 + 2 2008
A+B = 2(A+B)–(A+B) = - 2 2008 - 1
=> A+2A = - 2 2008 - 1
=> 3A = - 2 2008 - 1
=> A = - ( 2 2008 - 1 ) 3
c, A = 7 + 7 3 + 7 5 + 7 7 + . . . + 7 1999
Đặt B = 7 2 + 7 4 + 7 6 + . . . + 7 1999 + 7 2000 = 7 ( 7 + 7 3 + 7 5 + 7 7 + . . . + 7 1999 ) = 7A
A+B = 7 + 7 2 + 7 3 + . . . + 7 1999 + 7 2000
7(A+B) = 7 2 + 7 3 + . . . + 7 1999 + 7 2000 + 7 2001
7(A+B) – (A+B) = ( 7 2 + 7 3 + . . . + 7 1999 + 7 2000 + 7 2001 ) – ( 7 + 7 2 + 7 3 + . . . + 7 1999 + 7 2000 )
6(A+B) = 7 2001 - 7
A+B = 7 2001 - 7 6
=> A + 7A = 7 2001 - 7 6 => 8A = 7 2001 - 7 6 => A = 7 2001 - 7 48
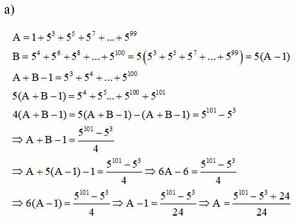
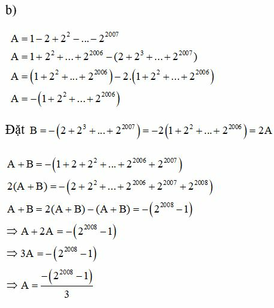
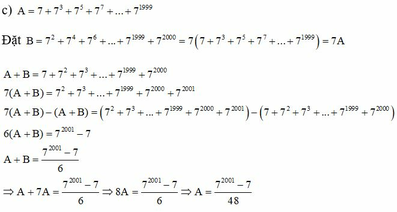
Ta có: \(5A=5-5^2+5^3-5^4+...+5^{99}-5^{100}\)
\(\Rightarrow5A+A=6A=1-5^{100}\)
\(\Rightarrow A=\dfrac{1-5^{100}}{6}\)
Mk làm hơi tắt một chút!!! Bn thông cảm nhé!
hơi tắt một chút nhưng mk chỉ suy luận câu câu trả lời của bạn một tí rồi cũng ra mà.
Cảm ơn bạn nhé