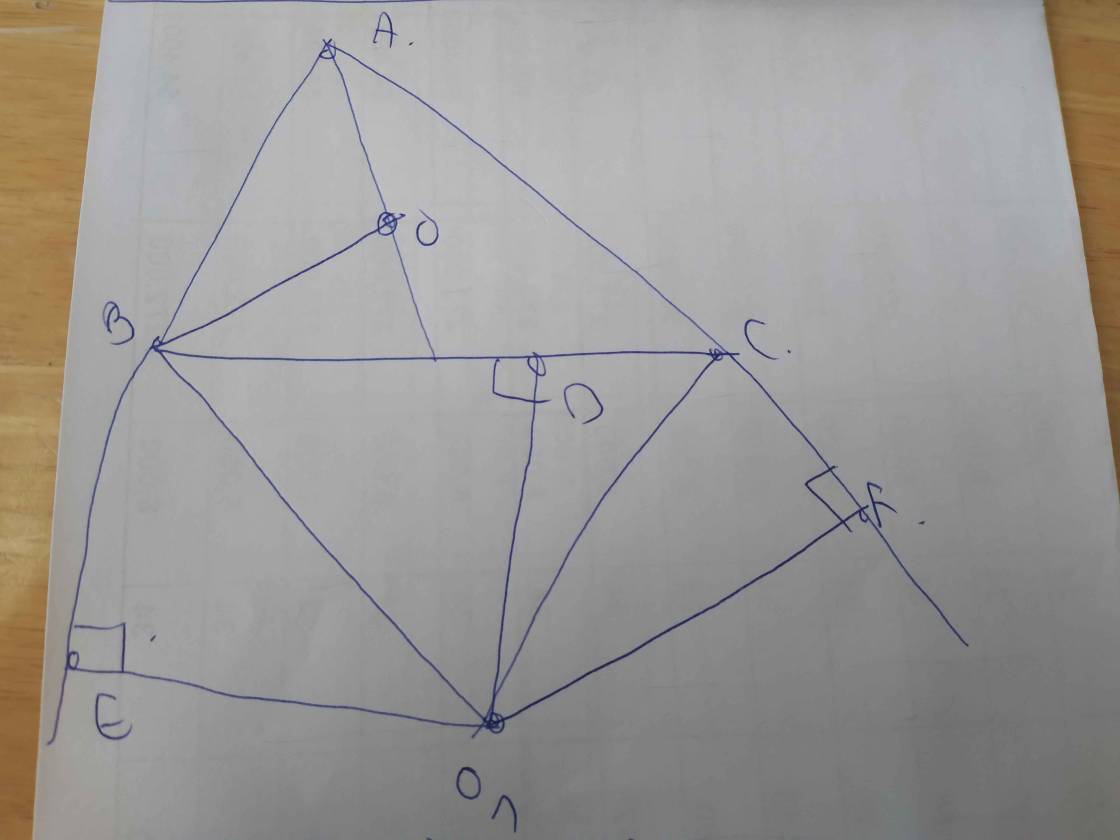
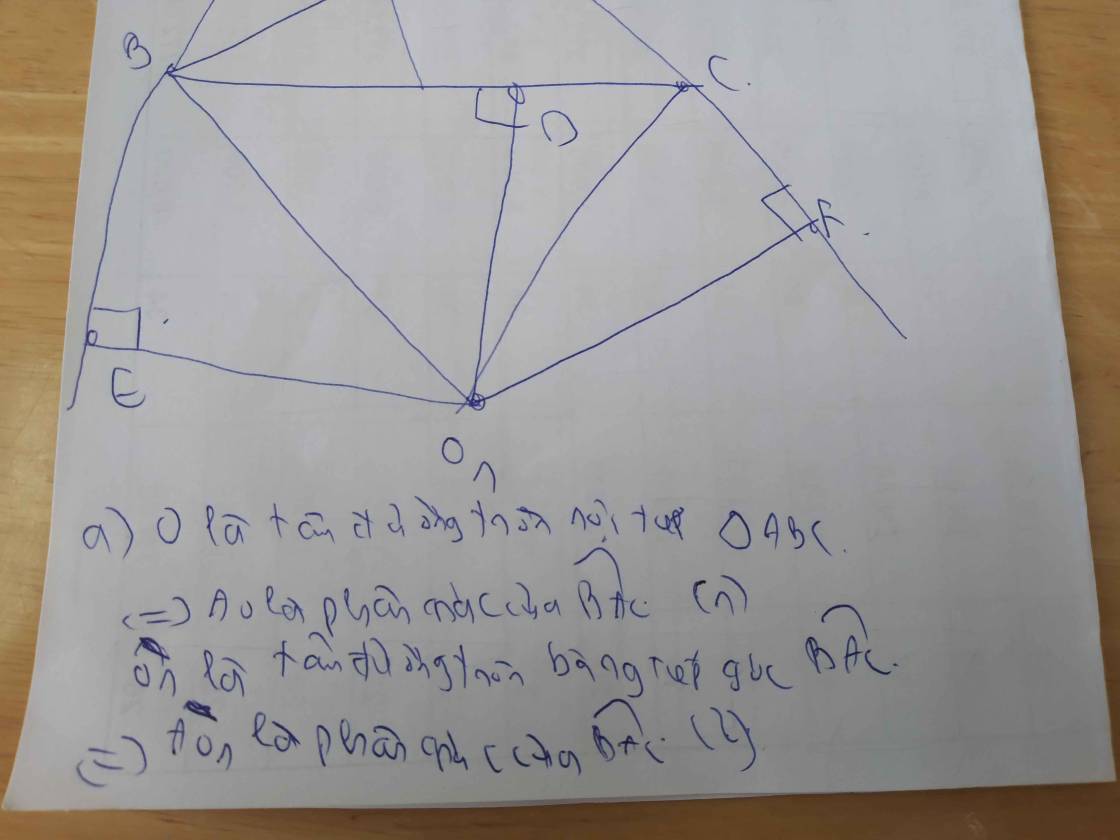
cho tam giac ABC nội tiếp đường tròn (O) ba đường phân giác trong của các góc A,B,C kéo dài lần lượt cắt đường tròn ngoại tiếp tại A1,B1,C1.đường tròn nội tiếp (I) tiếp xúc với ba cạnh BC,AC,AB tại A2,B2,C2.
a) chứng minh rằng : véc tơ OI = véc tơ OA1 + véc tơ OB1 +véc tơ OC1
b) chứng minh đường thẳng OI chính là đường thẳng Ơ-le của tam giác A2B2C2.





ở đây ko có lớp 10 đâu.
Bổ đề: Nếu tam giác ABC có tâm đường tròn ngoại tiếp O và trực tâm H thì \(\vec{OH}=\vec{OA}+\vec{OB}+\vec{OC}\).
Chứng minh: Xét hiệu \(\vec{s}=\vec{OA}+\vec{OB}+\vec{OC}-\vec{OH}=\left(\vec{OA}+\vec{OB}\right)+\vec{HA}\), có phương vuông góc với BC, tương tư vector s có phương vuông góc với CA. vậy vector s vuông góc với hai phương khác nhau nên là vector không.
Bằng cách tính góc, ta có \(IA_1\perp B_1C_1,IB_1\perp A_1C_1\to\) I chính là trực tâm tam giác A1B1C1. Từ đó áp dụng bổ đề 1, cho ta ngay a)
b) Ta có \(\vec{OA_1}=\frac{R}{r}\vec{IA_2},\vec{OB_1}=\frac{R}{r}\vec{IB_2},\vec{OC_1}=\frac{R}{r}\vec{IC_2}\to\vec{OA_1}+\vec{OB_1}+\vec{OC_1}\)
\(=\frac{R}{r}\left(\vec{IA_2}+\vec{IB_2}+\vec{IC_2}\right)=3\frac{R}{r}\vec{IG'}\) trong đó G' là trọng tâm tam giác A2B2C2. Theo câu a, ta suy ra véc tơ OI bằng 3R/r lần véc tơ IG', do đó điểm O nằm trên đường thẳng IG'. Vì I là tâm đường tròn ngoại tiếp tam giác A2B2C2 và G' là trọng tâm nên IG' chính là đường thẳng Ơ-le của tam giác A2B2C2. Suy ra OI chính là đường thẳng Ơ le của tam giác A2B2C2