Hãy giải phương trình: 2x2 + 5x + 2 = 0 theo các bước như ví dụ 3 trong bài học.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(Lưu ý: Các phần giải thích các bạn có thể không trình bày vào bài làm)
2 x 2 + 5 x + 2 = 0 ⇔ 2 x 2 + 5 x = − 2
(Chuyển 2 sang vế phải)
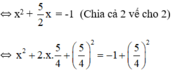
(Tách 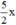 thành
thành 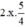 và thêm bớt
và thêm bớt 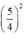 để vế trái thành bình phương).
để vế trái thành bình phương).
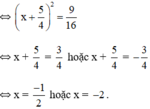
Vậy phương trình có hai nghiệm 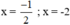

(Lưu ý: Các phần giải thích các bạn có thể không trình bày vào bài làm)
2x2 + 5x + 2 = 0
⇔ 2x2 + 5x = -2 (Chuyển 2 sang vế phải)
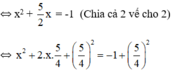
(Tách 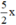 thành
thành 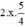 và thêm bớt
và thêm bớt 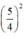 để vế trái thành bình phương).
để vế trái thành bình phương).
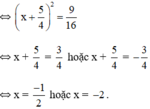
Vậy phương trình có hai nghiệm 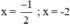

\(2x^2+5x+2=0\)
\(\Rightarrow2x^2+5x+\frac{50}{16}-\frac{18}{16}=0\)
\(\Rightarrow2\left(x^2+2.\frac{5}{4}x+\frac{25}{16}\right)=\frac{9}{8}\)
\(\Rightarrow\left(x+\frac{5}{4}\right)^2=\frac{9}{16}\)
\(\Rightarrow\orbr{\begin{cases}x+\frac{5}{4}=\frac{3}{4}\\x+\frac{5}{4}=\frac{-3}{4}\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x=-\frac{1}{2}\\x=-2\end{cases}}\)
Ta có :
\(2x^2+5x+2=0\)
\(\Leftrightarrow2x^2+5x=-2\)
\(\Leftrightarrow x^2+\frac{5}{2}x=-1\)
\(\Leftrightarrow x^2+2.x.\frac{5}{4}=-1\)
\(\Leftrightarrow x^2+2.x.\frac{5}{4}+\left(\frac{5}{4}\right)^2=-1+\left(\frac{5}{4}\right)^2\)
\(\Leftrightarrow\left(x+\frac{5}{4}\right)^2=-1+\frac{25}{16}\)
\(\Leftrightarrow\left(x+\frac{5}{4}\right)^2=\frac{9}{16}\)
\(\Leftrightarrow\orbr{\begin{cases}x+\frac{5}{4}=\frac{3}{4}\\x+\frac{5}{4}=-\frac{3}{4}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{2}\\x=-2\end{cases}}}\)
Vậy phương trình đã cho có hai nghiệm là........

Các bước chủ yếu để giải phương trình trong ví dụ 1:
- Thực hiện phép tính để bỏ dấu ngoặc
- Chuyển các hạng tử chứa ẩn sang một vế, các hằng số sang vế kia
- Thu gọn và giải phương trình nhận được
Các bước chủ yếu để giải phương trình trong ví dụ 2:
- Quy đồng mẫu hai vế
- Nhân hai vế với mẫu để khử mẫu
- Chuyển các hạng tử chứa ẩn sang một vế, các hằng số sang vế kia
- Thu gọn và giải phương trình nhận được

a) PT bậc nhất một ẩn là: x-2=0; 4-0,2x=0
b) Giải:
x-2=0 (*)
⟺ x=-2
Vậy tập nghiệm của pt (*) là S={-2}
4-0,2x=0 (**)
⟺-0,2x=-4
⟺x=-4/-0,2=20
Vậy tập nghiệm của pt (**) là S={20}

a: \(\Leftrightarrow\left(-x+3\right)\left(x+6\right)=18\)
\(\Leftrightarrow-x^2-6x+3x+18-18=0\)
\(\Leftrightarrow-x\left(x+3\right)=0\)
=>x=0 hoặc x=-3
b: \(\Leftrightarrow x\left(3x^2+6x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\3x^2+6x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2+2x-\dfrac{4}{3}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\\left(x+1\right)^2=\dfrac{7}{3}\end{matrix}\right.\Leftrightarrow x\in\left\{0;\dfrac{\sqrt{21}}{3}-1;\dfrac{-\sqrt{21}}{3}-1\right\}\)
c: =>x(3x-5)=0
=>x=0 hoặc x=5/3
d: =>(x-2)(x+2)=0
=>x=2 hoặc x=-2

1) Ta có: \(x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
Vậy: S={2}
Bài giải
2x2 + 5x + 2 = 0 ⇔ 2x2 + 5x = -2 ⇔ x2 + x = -1
x = -1
⇔ x2 + 2 . x . +
+ 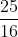 = -1 +
= -1 + 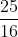 ⇔ (x +
⇔ (x +  )2 =
)2 = 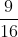
=> x + =
=  => x =
=> x = 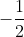
Hoặc x + =
= 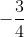 => x = -2.
=> x = -2.