tìm x biết: x4 -6x3 +9x2+2=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 10 2021
\(a,\Leftrightarrow x^2\left(x-4\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\\ b,\Leftrightarrow\left(3x-5\right)^2=0\Leftrightarrow x=\dfrac{5}{3}\)
TT
1
TM
1 tháng 8 2023
(a) \(9x^2+12x+4=0\)
\(\Leftrightarrow\left(3x+2\right)^2=0\Leftrightarrow3x+2=0\Leftrightarrow x=-\dfrac{3}{2}\)
(b) \(x^2+\dfrac{1}{4}=x\)
\(\Leftrightarrow x^2-x+\dfrac{1}{4}=0\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2=0\Leftrightarrow x-\dfrac{1}{2}=0\Leftrightarrow x=\dfrac{1}{2}\)
(c) \(4-\dfrac{12}{x}+\dfrac{9}{x^2}=0\left(x\ne0\right)\)
\(\Leftrightarrow\left(2-\dfrac{3}{x}\right)^2=0\Leftrightarrow2-\dfrac{3}{x}=0\Leftrightarrow x=\dfrac{3}{2}\)
CM
31 tháng 3 2019
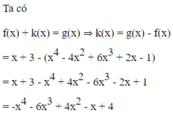
Nhận thấy số hạng có lũy thừa cao nhất của biến là - x 4 nên hệ số cao nhất là -1
Chọn đáp án A
30 tháng 4 2022
a: \(P\left(x\right)=6x^3+4x^2+2x-4\)
\(Q\left(x\right)=-x^4+6x^3-4x^2+3x-8\)
b: \(P\left(x\right)-Q\left(x\right)=x^4+8x^2-x+4\)
\(P\left(x\right)+Q\left(x\right)=-x^4+12x^3+5x-12\)
LH
7 tháng 6 2018
\(x^4+9x^2=0\left(1\right)\\ < =>x^2\left(x^2+9\right)=0\\ < =>\left[{}\begin{matrix}x^2=0\\x^2+9=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x^2+9=0\left(2\right)\end{matrix}\right.\)
có
\(x^2\ge0\forall x\\ =>x^2+9>0\)
mâu thuẫn với (2)
=> (2) vô nghiệm
vậy ...
H
1
9 tháng 11 2021
\(a,=\left(6x^3+3x^2-10x^2-5x+4x+2\right):\left(2x+1\right)\\ =\left(2x+1\right)\left(3x^2-5x+2\right):\left(2x+1\right)=3x^2-5x+2\\ b,=\left(x^4-2x^3+3x^2+x^3-2x^2+3x\right):\left(x^2-2x+3\right)\\ =\left(x^2-2x+3\right)\left(x^2+x\right):\left(x^2-2x+3\right)=x^2+x\)
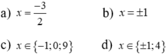
Ta có:
\(x^4-6x^3+9x^2+2\)
= \(x^2\left(x^2-6x+9\right)+2\)
= \(x^2\left(x^2-3x-3x+9\right)+2\)
= \(x^2\left[x\left(x-3\right)-3\left(x-3\right)\right]+2\)
= \(x^2\left[\left(x-3\right)\left(x-3\right)\right]+2\)
= \(x^2\cdot\left(x-3\right)^2+2\)
Ta lại có: \(x^2\ge0\) và \(\left(x-3\right)^2\ge0\) (với mọi x)
\(\Rightarrow x^2\cdot\left(x-3\right)^2+2\ge2\) (với mọi x)
hay \(x^4-6x^3+9x^2+2\ge2>0\)(với mọi x)
Vậy x \(\in\varnothing\)
Khó mò mãi mà ko ra dc lúc tra máy tính nó báo:"Can not Stove"