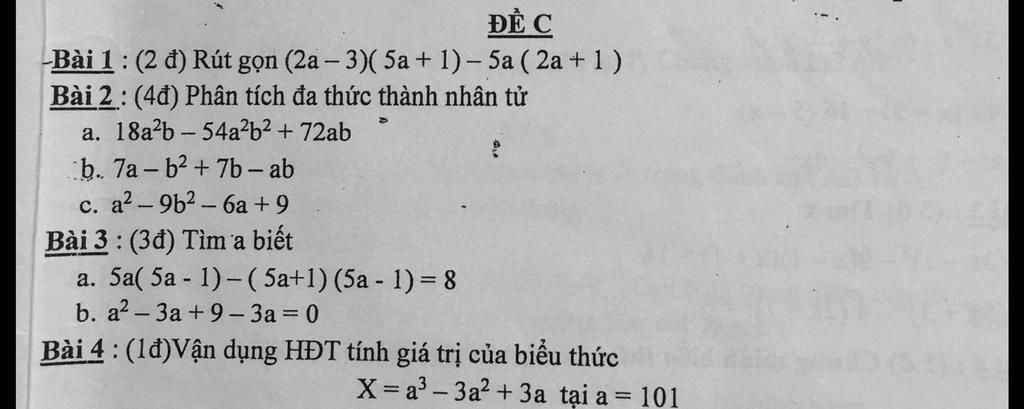
giúp e bài 2, 3, 4 với mn ko bỏ bước ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 8 2021
e: Ta có: \(2x\left(x-5\right)-26=x\left(2x+3\right)\)
\(\Leftrightarrow2x^2-10x-26-2x^2-3x=0\)
\(\Leftrightarrow-13x=26\)
hay x=-2
f: Ta có: \(x^2-9=-2x\left(x-3\right)\)
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)+2x\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(3x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
g: Ta có: \(4x^3-9x=0\)
\(\Leftrightarrow x\left(2x-3\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
h: Ta có: \(x^2-8x+2\left(x-8\right)=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
NT
25 tháng 8 2021
e. \(2x\left(x-5\right)-26=x\left(3+2x\right)\)
\(\Leftrightarrow2x^2-10x-26=3x+2x^2\)
\(\Leftrightarrow2x^2-10x-3x-2x^2=26\)
\(\Leftrightarrow-13x=26\) \(\Leftrightarrow x=-2\)
g. \(4x^3-9x=0\)
\(\Leftrightarrow x\left(4x^2-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\4x^2-9=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=\dfrac{9}{4}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm\dfrac{3}{2}\end{matrix}\right.\)
i. \(x^3-5x=0\)
\(\Leftrightarrow x\left(x^2-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-5=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=5\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm\sqrt{5}\end{matrix}\right.\)
k. \(x^2=10x-25\)
\(\Leftrightarrow x^2-10x+25=0\)
\(\Leftrightarrow\left(x-5\right)^2=0\)
\(\Leftrightarrow x-5=0\)
\(\Leftrightarrow x=5\)
f. \(x^2-9=-2x\left(x-3\right)\)
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)=-2x\left(x-3\right)\)
\(\Leftrightarrow x+3=-2x\)
\(\Leftrightarrow3x=-3\)
\(\Leftrightarrow x=-1\)
h. \(x^2-8x+2\left(x-8\right)=0\)
\(\Leftrightarrow x\left(x-8\right)+2\left(x-8\right)=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-8=0\\x+2=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
j. \(x\left(x-5\right)-x+5=0\)
\(\Leftrightarrow x\left(x-5\right)-\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\x-1=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\)
l. \(2x^3-72x=0\)
\(\Leftrightarrow2x\left(x^2-36\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-36=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=36\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm6\end{matrix}\right.\)
TG
31 tháng 5 2021
Bài 5:
f(x) có 1 nghiệm x - 2
=> f (2) = 0
\(\Rightarrow a.2^2-a.2+2=0\)
\(\Rightarrow4a-2a+2=0\)
=> 2a + 2 = 0
=> 2a = -2
=> a = -1
Vậy:....
P/s: Mỗi lần chỉ đc đăng 1 câu hỏi thôi! Bạn vui lòng đăng bài hình trên câu hỏi khác nhé!
DB
31 tháng 5 2021
a)Ta có △MIP cân tại M nên ˆMNI=ˆMPIMNI^=MPI^
Xét △MIN và △MIP có:
ˆNMI=ˆPMINMI^=PMI^
MI : cạnh chung
ˆMNI=ˆMPIMNI^=MPI^
Nên △MIN = △MIP (c.g.c)
b)Gọi O là giao điểm của EF và MI
Vì △MNP là tam giác cân và MI là đường phân giác của △MIP
Suy ra MI đồng thời là đường cao của △MNP
Nên ˆMOE=ˆMOF=90oMOE^=MOF^=90o
Xét △MOE vuông tại O và △MOF vuông tại O có:
OM : cạnh chung
ˆEMO=ˆFMOEMO^=FMO^(vì MI là đường phân giác của △MIP và O∈∈MI)
Suy ra △MOE = △MOF (cạnh góc vuông – góc nhọn kề)
Nên ME = MF
Vậy △MEF cân
tham khảo
25 tháng 8 2021
Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
19 tháng 2 2022
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
H
0
bài 2, bài 3 ạ
17 tháng 8 2021
tiêu đề bài hai có nghĩa là j zậy bnnnnnnnnnnnnnnnn
mk nhát đọc đề quá
KH
8 tháng 5 2021
Hướng làm:
Thấy cả tử mẫu cộng lại đều bằng 2021 → Cộng thêm 1 rồi quy đồng với mỗi phân thức
\(\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\\ \Leftrightarrow\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\\ \Leftrightarrow\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}\right)=0\\ \Leftrightarrow x+2021=0\Leftrightarrow x=-2021\)
TM
8 tháng 5 2021
\(< =>\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\)
\(< =>\dfrac{x+2+2019}{2019}+\dfrac{x+3+2018}{2018}=\dfrac{x+4+2017}{2017}+\dfrac{x+2021}{2021}\)
\(< =>\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\)
\(< =>\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}=\right)=0\)
\(< =>x+2021=0< =>x=-2021\)
Vậy....
HT
3
Bài 2:
a:\(18a^2b-54a^2b^2+72ab\)
\(=18ab\left(a-3ab+4\right)\)
b: \(7a-b^2+7b-ab\)
\(=7\left(a+b\right)-b\left(a+b\right)\)
\(=\left(a+b\right)\left(7-b\right)\)
c: \(a^2-9b^2-6a+9\)
\(=\left(a-3\right)^2-9b^2\)
\(=\left(a-3-3b\right)\left(a-3+3b\right)\)
Bài 4:
Ta có: \(X=a^3-3a^2+3a\)
\(=a^3-3a^2+3a-1+1\)
\(=\left(a-1\right)^3+1\)
\(=100^3+1=1000001\)
Bài 3:
a: Ta có: \(5a\left(5a-1\right)-\left(5a+1\right)\left(5a-1\right)=8\)
\(\Leftrightarrow25a^2-5a-25a^2+1=8\)
\(\Leftrightarrow5a=-7\)
hay \(a=-\dfrac{7}{5}\)
b: Ta có: \(a^2-3a+9-3a=0\)
\(\Leftrightarrow a\left(a-3\right)-3\left(a-3\right)=0\)
\(\Leftrightarrow\left(a-3\right)^2=0\)
\(\Leftrightarrow a-3=0\)
hay a=3