Giải ra giúp...
Đọc tiếp
Giải ra giúp ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
83
2
S
16 tháng 1 2022
PTHH : 2Al + 6HCl --> 2AlCl3 + 3H2 ↑ (1)
nAlCl3 = \(\dfrac{m}{M}=\dfrac{13,35}{27+35,5.3}=0.1\left(mol\right)\)
Từ (1) => nHCl = 2nH2 = 0.2 (mol)
=> mHCl = n.M = 0.2 x 36.5 = 7.3 (g)
16 tháng 1 2022
\(PTHH:2Al+6HCl\rightarrow2AlCl_3+3H_2\\ n_{AlCl_3}=\dfrac{m}{M}=\dfrac{13,35}{133,5}=0,1\left(mol\right)\\ Theo.PTHH:n_{HCl}=3.n_{AlCl_3}=3.0,1=0,3\left(mol\right)\\ m_{HCl}=n.M=0,3.36,5=10,95\left(g\right)\)
ST
1
NN
13 tháng 4 2021
Hmm, nói đến cờ chắc là dấu hiệu của semaphore, thử mò xem :v
vẽ hình giúp e ạ có gì giải ra ạ em cảm ơn ạ=))
25 tháng 10 2023
10: Chọn B
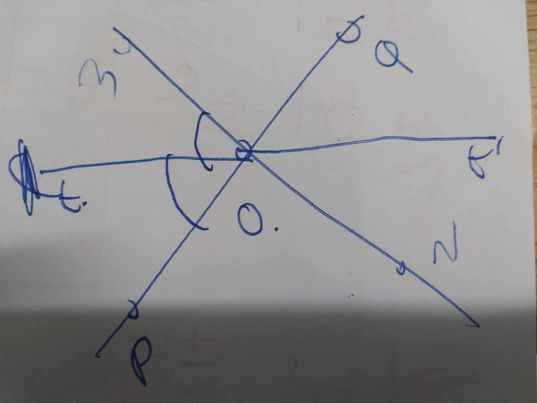
Ot là phân giác của \(\widehat{MOP}\)
=>\(\widehat{MOP}=2\cdot\widehat{tOP}\)
\(\widehat{MOP}=\widehat{NOQ}\)
=>\(\widehat{NOQ}=2\cdot\widehat{tOP}\)
mà \(\widehat{tOP}=\widehat{t'OQ}\)(hai góc đối đỉnh)
nên \(\widehat{NOQ}=2\cdot\widehat{t'OQ}\)
=>Ot' là phân giác của góc NOQ
11:
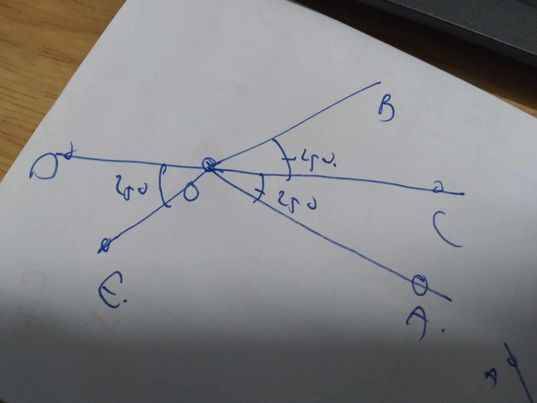
OC là phân giác của góc AOB
=>\(\widehat{AOC}=\widehat{BOC}=\dfrac{50^0}{2}=25^0\)
\(\widehat{DOE}=\widehat{BOC}\left(=25^0\right)\)
=>\(\widehat{DOE}+\widehat{DOB}=180^0\)
=>OB và OE là hai tia đối nhau
=>Hai góc đối đỉnh là \(\widehat{BOC};\widehat{DOE}\)
=>Chọn D
12:
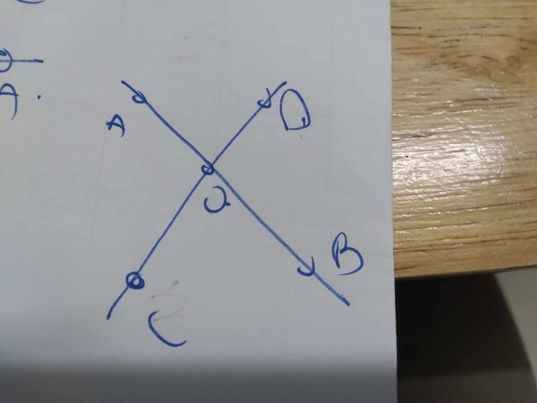
\(\widehat{AOC}+\widehat{AOD}=180^0\)
\(\widehat{AOC}-\widehat{AOD}=50^0\)
Do đó: \(\widehat{AOC}=\dfrac{180^0+50^0}{2}=115^0;\widehat{AOD}=115^0-50^0=65^0\)
=>\(\widehat{BOC}=\widehat{AOD}=65^0\)
=>Chọn B
18 tháng 10 2023
Xét tứ giác ABCD có:
A + B + C + D = 360 độ(theo định lý)
Suy ra C = 360 độ - ( A + B + D)
360 độ - 240 độ
120 độ
Vậy...
giải rõ ra giúp mình ạ
8 tháng 1 2022
a: Xét ΔADH vuông tại H và ΔADK vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)
Do đó: ΔADH=ΔADK
T
1
TK
26 tháng 9 2021
Bạn ghi đề thiếu mạch có dạng j nha
MCD :R1nt R2
\(U_2=U-U_1=6-2=4\left(V\right)\)
\(I=I_2=I_1=0,1\left(A\right)\)
\(R_1=\dfrac{U_1}{I_1}=\dfrac{2}{0,1}=20\left(\Omega\right)\)
\(R_2=\dfrac{U_2}{I_2}=\dfrac{4}{0,1}=40\left(\Omega\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
23.
Ta sẽ tìm điểm \(I\left(a;b;c\right)\) sao cho \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\) (1)
\(\left\{{}\begin{matrix}\overrightarrow{IA}=\left(-2-a;2-b;6-c\right)\\\overrightarrow{IB}=\left(-3-a;1-b;8-c\right)\\\overrightarrow{IC}=\left(-1-a;-b;7-c\right)\\\overrightarrow{ID}=\left(1-a;2-b;3-c\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\left(-5-4a;5-4b;24-4c\right)\)
(1) thỏa mãn khi: \(\left\{{}\begin{matrix}-5-4a=0\\5-4b=0\\24-4c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{4}\\b=\dfrac{5}{4}\\c=6\end{matrix}\right.\)
\(\Rightarrow I\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\)
Khi đó:
\(T=MA^2+MB^2+MC^2+MD^2=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IB}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IC}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{ID}\right)^2\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2+2\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}\right)\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2\) (do \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\))
\(IA^2+IB^2+IC^2+ID^2\) cố định nên \(T_{min}\) khi \(MI_{min}\)
\(\Leftrightarrow M\) trùng I
\(\Rightarrow M\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\Rightarrow x+y+z=-\dfrac{5}{4}+\dfrac{5}{4}+6=6\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
24.
\(a+b=4\Rightarrow b=4-a\)
ABCD là hình chữ nhật \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow C\left(a;a;0\right)\)
Tương tự ta có: \(C'\left(a;a;b\right)\)
M là trung điểm CC' \(\Rightarrow M\left(a;a;\dfrac{b}{2}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{A'B}=\left(a;0;-b\right)=\left(a;0;a-4\right)\\\overrightarrow{A'D}=\left(0;a;-b\right)=\left(0;a;a-4\right)\\\overrightarrow{A'M}=\left(a;a;-\dfrac{b}{2}\right)=\left(a;a;\dfrac{a-4}{2}\right)\end{matrix}\right.\)
Theo công thức tích có hướng:
\(\left[\overrightarrow{A'B};\overrightarrow{A'D}\right]=\left(-a^2+4a;-a^2+4a;a^2\right)\)
\(\Rightarrow V=\dfrac{1}{6}\left|\left[\overrightarrow{A'B};\overrightarrow{A'D}\right].\overrightarrow{A'M}\right|=\dfrac{1}{6}\left|a\left(-a^2+4a\right)+a\left(-a^2+4a\right)+\dfrac{a^2\left(a-4\right)}{2}\right|\)
\(=\dfrac{1}{4}\left|a^3-4a^2\right|=\dfrac{1}{4}\left(4a^2-a^3\right)\)
Xét hàm \(f\left(a\right)=\dfrac{1}{4}\left(4a^2-a^3\right)\) trên \(\left(0;4\right)\)
\(f'\left(a\right)=\dfrac{1}{4}\left(8a-3a^2\right)=0\Rightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\a=\dfrac{8}{3}\end{matrix}\right.\)
\(\Rightarrow f\left(a\right)_{max}=f\left(\dfrac{8}{3}\right)=\dfrac{64}{27}\)
MN
1
AH
Akai Haruma
Giáo viên
30 tháng 5 2021
Lời giải:
HPT \(\Leftrightarrow \left\{\begin{matrix} xy+4x-5y-20=xy+x-4y-4\\ xy-3x+y-3=xy-2x-y+2\end{matrix}\right.\)
\( \Leftrightarrow \left\{\begin{matrix} 3x-y=16\\ -x+2y=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\frac{37}{5}\\ y=\frac{31}{5}\end{matrix}\right.\)
Khi đó: \(m+2n=\frac{37}{5}+2.\frac{31}{5}=\frac{99}{5}\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 6 2021
Do AB bằng cạnh lục giác đều nội tiếp \(\Rightarrow\widehat{AOB}=\dfrac{1}{6}.360^0=60^0\)
\(\Rightarrow\Delta ABC\) đều \(\Rightarrow\left\{{}\begin{matrix}AB=OA=R\\OH=\dfrac{AB\sqrt{3}}{2}=\dfrac{R\sqrt{3}}{2}\end{matrix}\right.\)
Dây CD bằng cạnh tam giác đều nội tiếp \(\Rightarrow\widehat{COD}=\dfrac{1}{3}.360^0=120^0\Rightarrow\widehat{COK}=60^0\)
\(\Rightarrow\left\{{}\begin{matrix}CD=2CK=2OC.sin\widehat{COK}=R\sqrt{3}\\OK=OC.cos\widehat{COK}=\dfrac{R}{2}\end{matrix}\right.\)
\(\Rightarrow HK=OH-OK=\dfrac{R}{2}\left(\sqrt{3}-1\right)\)
\(S=\dfrac{1}{2}\left(AB+CD\right).HK=\dfrac{R^2}{2}\) (chắc có sự nhầm lẫn trong đáp án, không có hằng số \(\pi\) nào ở đây)
\(\frac{a+b}{b^2}\sqrt{\frac{a^2b^4}{a^2+2ab+b^2}}=\frac{a+b}{b^2}\cdot\frac{\sqrt{a^2b^4}}{\sqrt{\left(a+b\right)^2}}=\frac{a+b}{b^2}\cdot\frac{ab^2}{a+b}=a\)
à quên sửa chỗ này:)
\(=\frac{a+b}{b^2}\cdot\frac{\left|a\right|b^2}{a+b}=\left|a\right|\)xin lỗi nhé :v