Trong không gian cho 3 vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) đều khác vectơ - không. Khi nào ba vectơ đó đồng phẳng ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 9 2023
Tham khảo:
a) Đúng vì vectơ \(\overrightarrow 0 \) cùng hướng với mọi vectơ.
b) Sai. Chẳng hạn: Hai vecto không cùng hướng nhưng cũng không ngược hướng (do chúng không cùng phương).
c) Đúng.
\(\overrightarrow a \) và \(\overrightarrow b \) đều cùng phương với \(\overrightarrow c \) thì a // c và b // c do đó a // b tức là \(\overrightarrow a \)và \(\overrightarrow b \) cùng phương.
d) Đúng.
\(\overrightarrow a \) và \(\overrightarrow b \) đều cùng hướng với \(\overrightarrow c \) thì \(\overrightarrow a \)và \(\overrightarrow b \) cùng phương , cùng chiều đo đó cùng hướng.
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a)
+) Vectơ \(\overrightarrow a \) cùng phương với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow a \) song song với giá của vectơ \(\overrightarrow c \)
+) Vectơ \(\overrightarrow b \) cùng phương với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow b \) song song với giá của vectơ \(\overrightarrow c \)
Suy ra giá của vectơ \(\overrightarrow a \) và vectơ \(\overrightarrow b \) song song với nhau nên \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương
Vậy khẳng định trên đúng
b) Giả sử vectơ \(\overrightarrow c \) có hướng từ A sang B
+) Vectơ \(\overrightarrow a \) ngược hướng với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow a \) song song với giá của vectơ \(\overrightarrow c \) và có hướng từ B sang A
+) Vectơ \(\overrightarrow b \) ngược hướng với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow b \) song song với giá của vectơ \(\overrightarrow c \) và có hướng từ B sang A
Suy ra, hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng
Vậy khẳng định trên đúng
CM
14 tháng 1 2018
Ba vectơ a → ; b → v à c → đồng phẳng nếu thỏa mãn một trong hai điều kiện sau:
- Giá của 3 vector đều cùng song song với mặt phẳng (P).
- 1 trong 3 vec tơ biểu diễn được qua hai vec tơ còn lại,
tức là tồn tại cặp số (m; n) duy nhất thỏa mãn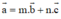 
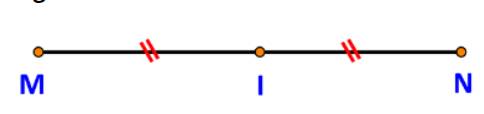
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a) Các vectơ đó là: \(\overrightarrow {MI} ,\overrightarrow {IM} ,\overrightarrow {IN} ,\overrightarrow {NI} ,\overrightarrow {MN} ,\overrightarrow {NM} \).
b) Dễ thấy:
+) vectơ \(\overrightarrow {IN} \)cùng hướng với vectơ \(\overrightarrow {MI} \). Hơn nữa: \(|\overrightarrow {IN} |\; = IN = MI = \;|\overrightarrow {MI} |\)
\( \Rightarrow \overrightarrow {IN} = \overrightarrow {MI} \)
+) vectơ \(\overrightarrow {IM} \)cùng hướng với vectơ \(\overrightarrow {NI} \). Hơn nữa: \(|\overrightarrow {IM} |\; = IM = NI = \;|\overrightarrow {NI} |\)
\( \Rightarrow \overrightarrow {IM} = \overrightarrow {NI} \)
Vậy \(\overrightarrow {IN} = \overrightarrow {MI} \) và \(\overrightarrow {IM} = \overrightarrow {NI} \).
BT
19 tháng 5 2017
Có \(\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.cos\left(\overrightarrow{a},\overrightarrow{b}\right)\).
Vì vậy:
\(\overrightarrow{a}.\overrightarrow{b}< 0\) khi \(cos\left(\overrightarrow{a},\overrightarrow{b}\right)< 0\) hay \(90^o< \left(\overrightarrow{a},\overrightarrow{b}\right)\le180^o\).
\(\overrightarrow{a}.\overrightarrow{b}>0\) khi \(cos\left(\overrightarrow{a},\overrightarrow{b}\right)>0\) hay \(0^o\le\left(\overrightarrow{a},\overrightarrow{b}\right)< 90^o\).
\(\overrightarrow{a}.\overrightarrow{b}=0\) khi \(cos\left(\overrightarrow{a},\overrightarrow{b}\right)=0\) hay \(\left(\overrightarrow{a},\overrightarrow{b}\right)=90^o\).
27 tháng 5 2017
\(\overrightarrow{m}=\left(-4;-2;3\right);\overrightarrow{n}=\left(-9;2;1\right)\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Do các vectơ đều nằm trên đường thẳng AB nên các vectơ này đều cùng phương với nhau.
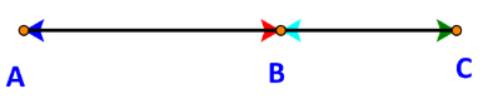
Dễ thấy:
Các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BC} \) cùng hướng (từ trái sang phải.)
Các vectơ \(\overrightarrow {BA} ,\overrightarrow {CA} ,\overrightarrow {CB} \) cùng hướng (từ phải sang trái.)
Do đó, các cặp vectơ cùng hướng là:
\(\overrightarrow {AB} \) và \(\overrightarrow {AC} \); \(\overrightarrow {AC} \) và \(\overrightarrow {BC} \); \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \); \(\overrightarrow {BA} \) và \(\overrightarrow {CA} \); \(\overrightarrow {BA} \) và \(\overrightarrow {CB} \);\(\overrightarrow {BA} \) và \(\overrightarrow {CB} \).
Các cặp vectơ ngược hướng là:
\(\overrightarrow {AB} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CB} \);
\(\overrightarrow {AC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CB} \);
\(\overrightarrow {BC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CB} \);
Thỏa mãn :
- Giá của 3 vector đều song song với mặt phẳng (P) nên chúng đồng phẳng
- Khi ba vectơ có giá của chúng cùng song song với một mặt phẳng