Cho 3 đường thẳng \(d_1;d_2;d_3\) không cùng nằm trong một mặt phẳng và cắt nhau từng đôi một. Chứng minh ba đường thẳng trên đồng quy ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
30 tháng 1 2021
Lời giải:
$M\in d_1$ nên gọi tọa độ của $M$ là $(2a+3,a)$
Khoảng cách từ $M$ đến $(d_2)$ là:\(\frac{|2a+3+a+1|}{\sqrt{1^2+1^2}}=\frac{1}{\sqrt{2}}\Leftrightarrow |3a+4|=1\Leftrightarrow 3a+4=\pm 1\)
\(\Leftrightarrow a=-1; a=\frac{-5}{3}\)
Thay vào ta có tọa độ của điểm $M$
MH
30 tháng 1 2021
Lấy \(M\in d_1\Rightarrow M\left(2y+3;y\right)\)
Ta có: \(d\left(M;d_2\right)=\dfrac{1}{\sqrt{2}}\Leftrightarrow\dfrac{\left|2y+3+y+1\right|}{\sqrt{1^2+1^2}}=\dfrac{1}{\sqrt{2}}\)
\(\Leftrightarrow\dfrac{\left|3y+4\right|}{\sqrt{2}}=\dfrac{1}{\sqrt{2}}\Leftrightarrow\left|3y+4\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}3y+4=1\\3y+4=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=1\\y=-\dfrac{5}{3}\end{matrix}\right.\)
\(y=1\Rightarrow M\left(5;1\right)\)
\(y=-\dfrac{5}{3}\Rightarrow M\left(-\dfrac{1}{3};-\dfrac{5}{3}\right)\)
29 tháng 10 2023
Tọa độ giao điểm của (d2) và (d3) là nghiệm của hệ phương trình sau:
\(\left\{{}\begin{matrix}x+1=-x+3\\y=x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Thay x=1 và y=2 vào (d1), ta được:
\(\left(m^2-1\right)+m^2-5=2\)
=>\(2m^2=8\)
=>\(m^2=4\)
=>\(\left[{}\begin{matrix}m=2\\m=-2\end{matrix}\right.\)
12 tháng 9 2023
- Vẽ đồ thị hàm số \(y = x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{1} = - 3\) ta được điểm \(B\left( { - 3;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
- Vẽ đồ thị hàm số \(y = - x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{{ - 1}} = 3\) ta được điểm \(C\left( {3;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = - x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(C\).
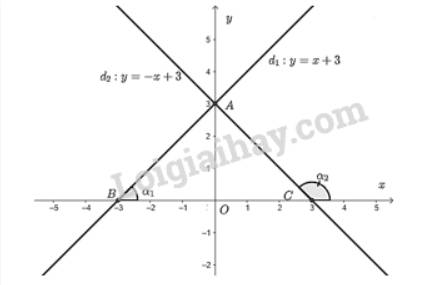
Từ đồ thị ta thấy giao điểm của hai đường thẳng là \(A\left( {0;3} \right)\).
Đường thẳng \({d_1}\) cắt trục \(Ox\) tại \(B\left( { - 3;0} \right)\).
Đường thẳng \({d_2}\) cắt trục \(Oy\) tại \(C\left( {3;0} \right)\).
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 11 2019
a/ \(y=-2x-5\)
\(\Rightarrow\left\{{}\begin{matrix}2m=-2\\m-1=-5\end{matrix}\right.\) \(\Rightarrow\) không tồn tại m thỏa mãn
b/ \(y=x-2\)
\(\Rightarrow2m.1=-1\Rightarrow m=-\frac{1}{2}\)
Bài 2:
Hệ phương trình tọa độ giao điểm M:
\(\left\{{}\begin{matrix}y=3x-2\\2y-x=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\) \(\Rightarrow M\left(1;1\right)\)
Bài 3:
Hệ pt tọa độ giao điểm A của d1 và d2:
\(\left\{{}\begin{matrix}y=2x-3\\y=x-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\) \(\Rightarrow A\left(2;1\right)\)
Để 3 đường thẳng đồng quy \(\Leftrightarrow d_3\) qua A
\(\Rightarrow\left(m-1\right).2+2=1\Rightarrow m=\frac{1}{2}\)
29 tháng 8 2023
a: 
b: Phương trình hoành độ giao điểm là:
2x-1=x+2
=>x=3
Thay x=3 vào y=x+2, ta được:
y=3+2=5
c: Vì (d)//(d1) nên (d): y=2x+b
Thay x=1 và y=0 vào (d), ta được:
b+2=0
=>b=-2
=>y=2x-2
12 tháng 9 2023
Gọi \({\alpha _1};{\alpha _2}\) lần lượt là 2 góc tạo bởi đường thẳng \({d_1};{d_2}\) với \(Ox\).
Dùng thước đo độ ta kiểm tra được\({\alpha _1} = 45^\circ ;{\alpha _2} = 135^\circ \).
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 10 2020
a/ Gọi A là giao điểm d1 và d2 \(\Rightarrow\) pt hoành độ của A:
\(x+2=5-2x\Rightarrow3x=3\Rightarrow x=1\Rightarrow y=3\)
\(\Rightarrow A\left(1;3\right)\)
Thay tọa độ A vào pt d3: \(3=3.1\) (thỏa mãn) \(\Rightarrow A\in d_3\)
Vậy d1, d2, d3 đồng quy tại A
b/ Để \(d_1;d_2;\Delta\) đồng quy \(\Leftrightarrow\Delta\) đi qua A
\(\Leftrightarrow3=m.1+m-5\Rightarrow m=4\)
31 tháng 12 2021
b: Để hai đường thẳng cắt nhau tại một điểm trên trục tung thì m-1=15
hay m=16
Gọi
, 
, 
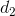là ba đường thẳng đã cho. Gọi I =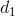 
∩ 
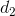
Ta chứng minh I ∈
I ∈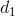
=> I ∈ (β) = ( 
, 
)
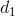I ∈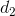
=> I ∈ (ɣ) = ( 
, 
)
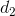Từ đó suy ra, I ∈