Bài tập 72 trang 37.Sgk Toán lớp 6 tập 2
HELP ME!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
5
5 tháng 4 2018
Ví dụ 2x+7-5= 28
=> 2x+7=28-5
=>2x+7=23
=>2x =23-7
=>2x =16
=>x =16:2
=> x =8
15 tháng 1 2018
?1 :
a) Điểm -5 nằm ..bên trái.. điểm -3, nên -5 < -3, và viết : -5 < -3.
b) Điểm 2 nằm ..bên phải.. điểm -3, nên 2 > -3, và viết : 2 > -3.
c) Điểm -2 nằm ..bên trái.. điểm 0, nên -2 < 0, và viết : -2 < 0.
15 tháng 1 2018
Vì phần tử của A là số tự nhiên lớn hơn 8 và nhỏ hơn 14 không thuoccj tập hợp A
Vậy A = { 9 ; 10 ; 11 ; 12 ; 13 }
Dùng tính chất đặc trưng cho các phần tử
\(A=\left\{x\in N,8< x< 14\right\}\)
Ta có : \(12\in A\)và \(16\notin A\)
30 tháng 3 2017
A=\(\dfrac{7}{19}\).\(\left(\dfrac{8}{11}+\dfrac{3}{11}\right)\)+\(\dfrac{12}{19}\)
A=\(\dfrac{7}{19}.1+\dfrac{12}{19}\)
A= \(\dfrac{7}{19}+\dfrac{12}{19}=1\)
B=\(\dfrac{5}{9}.\left(\dfrac{7}{13}+\dfrac{9}{13}-\dfrac{3}{13}\right)\)
B=\(\dfrac{5}{9}.1=\dfrac{5}{9}\)
HM
20 tháng 3 2016
Căn cứ vào tính chất giao hoán và tính chất kết hợp của phép nhân phân số.
Ví dụ: Tính chất giao hóa của phép nhân phân số:
Bằng cách tương tự, em hãy suy ra tính chất kết hợp của phép nhân phân số từ tính chất kết hợp của phép nhân số nguyên.
NQ
1
21 tháng 2 2021
Bài 37 trang 11 sách bài tập Toán 6 Tập 2: Bạn Minh đã tìm ra một cách "rút gọn" phân số rất đơn giản. Này nhé:
Em hãy kiểm tra xem các kết quả tìm được có đúng không?
Em có thể áp dụng "phương pháp" này để rút gọn các phân số có dạng ab/bc hay không?
Lời giải:
Kiểm tra ta thấy các kết quả tìm được đều đúng. Tuy nhiên, không thể áp dụng "phương pháp" trên để rút gọn các phân số có dạng ab/bc.
Ví dụ : 
Cách "rút gọn" của bạn Minh chỉ đúng một cách ngẫu nhiên
12 tháng 4 2017
a) Bạn Cường đã đổi hỗn số sang phân số rồi cộng các phân số sau đó đổi kết quả sang hỗn số.
b) Cách tính nhanh hơn là: Cộng riêng phần nguyên cộng riêng phần phân số.
26 tháng 5 2020
2, \(\widehat{ABC} + \widehat{BCA} = \widehat{BAC} = 90^0 ⇒ \widehat{BCA} = 90^0 - \widehat{ABC}\)
\(\widehat{ABC} +\widehat{ BAH} = \widehat{BAC} =90^0⇒\widehat{BAH} = 90^0 - \widehat{ABC}\)
\(\widehat{BCA} = \widehat{BAH}\)
XÉT \(\bigtriangleup\)HBA và\(\bigtriangleup\) HAC có :
\(\widehat{BHA}=\widehat{BAC}=90^0\)
\(\widehat{BCA}=\widehat{BAH}\)
⇒ \(\bigtriangleup\)HBA ∼ \(\bigtriangleup\) HAC
b, Áp dụng hệ thức \(b^2=a.b'\) vào \(\bigtriangleup{ABC}\) vuông tại A , ta có :
\(AC^2=BC.CH\) (đpcm)
c, Áp dụng hệ thức \(h^2=b'.c'\) vào \(\bigtriangleup{ABC}\) vuông tại A, ta có :
\(AH^2=BH.CH\) (đpcm)
P
2
20 tháng 2 2022
tham khảo :
Giải Bài 6.26 trang 12 sách bài tập Toán 6 Kết nối tri thức với cuộc sống
NN
4
ví dụ :7/3 và 7/4
Bài 72 (trang 37 SGK Toán 6 tập 2):
Đố: Có những cặp phân số mà ta nhân chúng với nhau hoặc cộng chúng với nhau đều được cùng một kết quả.
Giải:
Giả sử ta chọn hai phân số có cùng tử: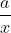
và 
.
Ta muốn có
.
Thế thì a . a = a.(x + y). Từ đó suy ra x + y = a.
Vì vậy với mỗi a > 1 cho trước ta có thể chọn x và y sao cho x + y = a.
Chẳng hạn với a = 11, x = 5, y = 6 ta có:
Mặt khác,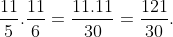
Vậy 
.
Như vậy ta có thể tìm được vô số cặp phân số mà tổng và tích của chúng bằng nhau.