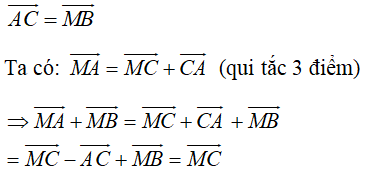Cho đoạn thẳng AB và điểm M nằm giữa A và B sao cho \(AM>MB\). Vẽ các vectơ \(\overrightarrow{MA}+\overrightarrow{MB}\) và \(\overrightarrow{MA}-\overrightarrow{MB}\) ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MA} + \overrightarrow {AM} = \overrightarrow {MM} = \overrightarrow 0 \) (vì vectơ \(\overrightarrow {MB} = - \overrightarrow {MA} = \overrightarrow {AM} .\))
b) Xét hình bình hành BGCD ta có: \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GD} \)
\( \Rightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GA} + \overrightarrow {GD} = \overrightarrow {DG} + \overrightarrow {GD} = \overrightarrow {{\rm{DD}}} = \overrightarrow 0 \)
(vì \(\overrightarrow {GA} = - \overrightarrow {GD} = \overrightarrow {DG} \))

Tham khảo:

a) M thuộc cạnh BC nên vectơ \(\overrightarrow {MB} \) và \(\overrightarrow {MC} \) ngược hướng với nhau.
Lại có: MB = 3 MC \( \Rightarrow \overrightarrow {MB} = - 3.\overrightarrow {MC} \)
b) Ta có: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} \)
Mà \(BM = \dfrac{3}{4}BC\) nên \(\overrightarrow {BM} = \dfrac{3}{4}\overrightarrow {BC} \)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {BC} \)
Lại có: \(\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} \) (quy tắc hiệu)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC} \)
Vậy \(\overrightarrow {AM} = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC} \)

Tham khảo:
a) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) ngược hướng

\( \Leftrightarrow \left\{ \begin{array}{l}AB//AM\\B \; \text {và}\; M \; \text {nằm cùng phía so với điểm A}\end{array} \right.\)
\( \Leftrightarrow \) A, B, thẳng hàng và A nằm giữa B và M
b) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) cùng phương
TH1: \(MA < MB\)
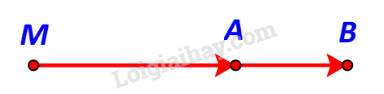
M, A, B thẳng hàng & A nằm giữa M và B.
TH2: \(MA > MB\)
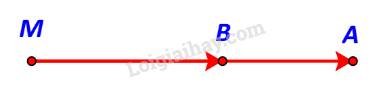
M, A, B thẳng hàng & B nằm giữa M và A.
c) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) cùng hướng
TH1: \(AM < AB\)

A, M, B thẳng hàng & M nằm giữa A và B.
TH2: \(AB < AM\)

A, M, B thẳng hàng & B nằm giữa A và M.
d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng

\( \Leftrightarrow \left\{ \begin{array}{l}MA//MB\\A \; \text {và} \; B\; \text {nằm về hai phía so với điểm M}\end{array} \right.\)
\( \Leftrightarrow \) A, M, B thẳng hàng & M nằm giữa A và B.
Vậy điều kiện cần và đủ để M nằm giữa A và B là d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng

a) \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{BM}=\overrightarrow{BA}\)
Vậy bất kì điểm M nào nằm trên mặt phẳng cũng thỏa mãn:
\(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{BA}\).
b) Do \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{BM}=\overrightarrow{BA}\) nên không tồn tại điểm M thỏa mãn: \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{AB}\).
c) \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}\) nên M là trung điểm của AB.
a,, CÓ \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{BA}\Leftrightarrow\overrightarrow{BA}=\overrightarrow{BA}\)
Vậy với mọi điểm M thì đều thõa mãn
b, có \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{AB}\Leftrightarrow\overrightarrow{BA}=\overrightarrow{AB}\) ( không thõa mãn)
vậy không có điểm M nào thõa mãn điều kện trên
c, có \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{O}\) \(\Rightarrow\) M là trung điểm của AB

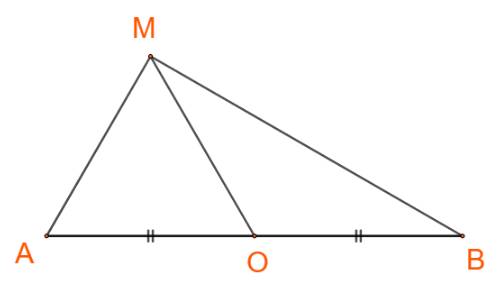
Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow 0 \Leftrightarrow - \overrightarrow {OA} = \overrightarrow {OB} \)
\(\Rightarrow {\overrightarrow {MO} ^2} - {\overrightarrow {OA} ^2} = \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right)\left( {\overrightarrow {MO} - \overrightarrow {OA} } \right) \\= \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right)\left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) = \overrightarrow {MA} .\overrightarrow {MB} \) (đpcm)

Gọi N là trung điểm AB
\(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{MA}-\overrightarrow{MB}\right|\)
\(\Leftrightarrow2\left|\overrightarrow{MN}\right|=\left|\overrightarrow{BA}\right|\)
\(\Leftrightarrow MN=\dfrac{a^2}{2}\)
\(\Rightarrow\Delta MAB\) vuông tại M
Áp dụng BĐT AM-GM:
\(\Rightarrow MH^2=HA.HB\le\dfrac{\left(HA+HB\right)^2}{4}=\dfrac{AB^2}{4}=\dfrac{a^2}{4}\)
\(\Rightarrow MH\le\dfrac{a}{2}\)

Kí hiệu v là vectơ nhé
1) Gọi I là điểm thỏa v IA + v IB + 3 v IC = 0 (1) (đây là vectơ 0 nhé)
=> v IA + v IA + v AB + 3 v IA + 3 AC = 0
=> 5 v IA = - (v AB + 3 v AC) => I cố định (do A, B, C cố định)
Ta có: v a = v MA + v MB + 3 v MC = v MI + v IA + v MI + v IB + 3 v MI + 3 v IB =
= 5 v MI + ( v IA + v IB + 3 v IC) = 5 v MI (do (1))
=> | v a| = | 5 v MI| = 5 MI
|v a| Min <=> MI min <=> MI = 0 <=> M trùng I
Vậy khi M là điểm thỏa 5 v MA = - (v AB + 3 v AC) (cố định) thì độ dài vectơ a nhỏ nhất.
Với mọi điểm O ta có :
\(\overrightarrow{u}=\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{2MC}=\overrightarrow{OA}-\overrightarrow{OM}+\overrightarrow{OB}-\overrightarrow{OM}+2\left(\overrightarrow{OC}-\overrightarrow{OM}\right)\)
\(=\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}-4\overrightarrow{OM}\)
Ta chọn điểm O sao cho \(\overrightarrow{v}=\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}=\overrightarrow{0}\)
( Chú ý: Nếu G là trọng tâm tam giác ABC thì \(\overrightarrow{v}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OC}=3\overrightarrow{OG}+\overrightarrow{OC}=4\overrightarrow{OG}+\overrightarrow{GC}\). Bởi vậy để \(\overrightarrow{v}=\overrightarrow{0}\)ta chọn điểm O sao cho \(\overrightarrow{GO}=\frac{1}{4}\overrightarrow{GC}\))
Khi đó \(\overrightarrow{u}=-4\overrightarrow{OM}\)và do đó \(|\overrightarrow{u}|=4OM\)
Độ dài vectơ \(\overrightarrow{u}\)nhỏ nhất khi và chỉ khi 4OM nhỏ nhất hay M là hình chiếu vuông góc của O trên d