Nêu các công thức biến đổi lượng giác đã học ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 1 2017
a) Các hằng đẳng thức lượng giác cơ bản:
sin2α + cos2α = 1
1 + tan2α = 1/(cos2α); α ≠ π/2 + kπ, k ∈ Z
1 + cot2α = 1/(sin2α); α ≠ kπ, k ∈ Z
tanα.cotα = 1; α ≠ kπ/2, k ∈ Z
b) Công thức cộng:
cos(a - b) = cosa cosb + sina sinb
cos(a + b) = cosa cosb - sina sinb
sin(a - b) = sina cosb - cosa sinb
sin(a + b) = sina.cosb + cosa.sinb
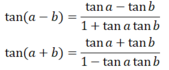
c) Công thức nhân đôi:
sin2α = 2 sinα cosα
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
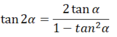
d) Công thức biến đổi tích thành tổng:
cos a cosb = 1/2 [cos(a - b) + cos(a + b) ]
sina sinb = 1/2 [cos(a - b) - cos(a + b) ]
sina cosb = 1/2 [sin(a - b) + sin(a + b) ]
Công thức biến đổi tổng thành tích:
29 tháng 7 2021
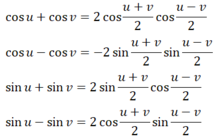
CÂU 1:
- Nhiệt lượng được hiểu là một phần nhiệt năng mà vật sẽ nhận được hay mất đi trong quá trình truyền nhiệt.
- Có hai cách làm thay đổi nhiệt năng của vật là:
+ Thực hiện công
+ Truyền nhiệt.
Câu 2:
- Công thức tính nhiệt lượng thu vào là: Q = m . c . ∆t
+ Q là nhiệt lượng (J)
+ m là khối lượng của vật (kg)
∆t là độ tăng nhiệt của vật (0C hoặc K)
c là nhiệt dung riêng của chất làm vật (J/kg.K).
29 tháng 7 2021
Câu 1 :
Nhiệt lượng là : phần nhiệt năng mà vật nhận thêm hay mất bớt đi trong quá trình truyền nhiệt
Có 2 cách làm thay đổi nhiệt năng : thực hiện công và truyền nhiệt
Câu 2 :
Công thức tính nhiệt lượng : Q = m . c . Δt
Trong đó : Q : là nhiệt lượng vật thu vào (j)
m : là khối lượng của vật (kg)
Δt : t2 - t1 là đọ tăng nhiệt độ của vật (C0)
c : là nhiệt dung riêng của vật (j/kg)
Chúc bạn học tốt
25 tháng 2 2016
a) Những điểm chung của các ngành :
- Vai trò : Đều là những ngành quan trọng ( công nghiệp trọng điểm), có vai trò to lớn cả về kinh tế và xã hội
- Nguồn lực : Tuy có những hạn chế nhưng đều có thế mạnh phát triển lâu dài
- Sự phát triển : nói chung, chúng đều khai thác được những lợi thế và phát triển mạnh
b) Thế mạnh để phát triển từng ngành
- Công nghiệp năng lượng
+ Tài nguyên dồi dào : than, dầu khí, thủy năng, nguồn năng lượng khác
+ Thị trường rộng lớn
+ Chính sách của Nhà nước và các thế mạnh khác : công nghiệp năng lượng được đầu tư phát triển đi trước một bước
- Công nghiệp chế biến nông, lâm, thủy sản
+ Nguyên liệu tại chỗ phong phú từ các ngành nông, lâm, thủy sản
+ Thị trường tiêu thụ rộng lớn
+ Chính sách phát triển và các thế mạnh khác : được quan tâm phát triển, thu hút đầu tư, lao động dồi dào,..
- Công nghiệp sản xuất hàng tiêu dùng
+ Nguồn lao động dồi dào, giàu kinh nghiệm
+ Thị trường tiêu thụ rộng lớn
+ Các nhân tố khác : được quan tâm phát triến, thu hút đầu tư
25 tháng 12 2022
a. Sự biến đổi bán kính nguyên tử khi điện tích hạt nhân tăng:
+ Trong cùng chu kỳ : bán kính giảm.
+ Trong cùng nhóm A : bán kính tăng
b. Sự biến đổi năng lượng ion hóa thứ nhất của các nguyên tố nhóm A: Khi điện tích hạt nhân tăng:
+ Trong cùng chu kỳ năng lượng ion hóa tăng.
+ Trong cùng nhóm, năng lượng ion hóa giảm.P/s:chúc bạn học tốt!
HN
2
8 tháng 11 2021
Tham khảo!
Chúng ta sẽ lấy ví dụ về một công thức đơn giản.
1.Trên trang tính, hãy bấm vào ô mà bạn muốn nhập công thức vào đó.
2.Nhập = (dấu bằng) trước các hằng số và toán tử (tối đa lên đến 8192 ký tự) mà bạn muốn sử dụng trong phép tính.
Ví dụ: nhập =1+1.
3.Nhấn Enter (Windows) hoặc Return (máy Mac).
Chúng ta hãy lấy một biến thể khác của một công thức đơn giản. Nhập =5+2*3 vào một ô khác, rồi nhấn Enter hoặc Return. Excel nhân hai số cuối rồi cộng với số thứ nhất thành kết quả.
VT
5 tháng 9 2018
Số đo độ biến thiên nội năng trong quá trình truyền nhiệt là nhiệt lượng: Q = ΔU
(đơn vị của Q và ΔU là Jun)
Công thức tính nhiệt lượng vật thu vào hay tỏa ra khi nhiệt độ của vật thay đổi:
Q = m.c.Δt; Trong đó c là nhiệt dung riêng (J/kg.K), Δt là độ tăng hoặc giảm của nhiệt độ (ºC hoặc K), m là khối lượng của vật (kg).
1.Công thức cộng:
sin(x+y)=sinx.cosy+cosx.siny
sin(x-y)=sinx.cosy-cosx.siny
cos(x+y)=cosxcosy-sinxsiny
cos(x-y)=cosxcosy+sinxsiny
tan(x+y)=\(\dfrac{tanx+tany}{1-tanx.tany}\)
tan(x-y)=\(\dfrac{tanx-tany}{1+tanx.tany}\)
2.Công thức nhân đôi:
sin2x=2sinx.cosx
cos2x=cos2x-sin2x=1-2sin2x=2cos2x-1
tan2x=\(\dfrac{2tanx}{1-tan^2x}\)
3. Công thức hạ bậc:
sin2x=\(\dfrac{1-cos2x}{2}\)
cos2x=\(\dfrac{1+cos2x}{2}\)
tan2x=\(\dfrac{1-cos^2x}{1+cos^2x}\)
4. Công thức biến đổi tích thành tổng:
cosx.cosy=\(\dfrac{1}{2}\)[cos(x-y)+cos(x+y)]
sinx.siny=\(\dfrac{1}{2}\)[cos(x-y)-cos(x+y)]
sinx.cosy=\(\dfrac{1}{2}\)[sin(x-y)+sin(x+y)]
5. Công thức biến đổi tổng thành tích:
cosx+cosy=2cos\(\dfrac{x+y}{2}\).cos\(\dfrac{x-y}{2}\)
cosx-cosy=2sin\(\dfrac{x+y}{2}\).sin\(\dfrac{x-y}{2}\)
sinx+siny=2sin\(\dfrac{x+y}{2}\).cos\(\dfrac{x-y}{2}\)
sinx-siny=2cos \(\dfrac{x+y}{2}\).sin \(\dfrac{x-y}{2}\)