Cho \(\tan a=2\)
Tính giá trị của biểu thức :
\(C=\dfrac{\sin a}{\sin^3a+2\cos^3a}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A.
Áp dụng công thức biến đổi tổng thành tích và công thức nhân đôi; ta có
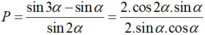


\(cot\alpha=3\Leftrightarrow\dfrac{cos\alpha}{sin\alpha}=3\Leftrightarrow cos\alpha=3sin\alpha\)
Khi đó:
\(\dfrac{3sin\alpha-2cos\alpha}{12sin^3\alpha+4cos^3\alpha}=\dfrac{3sin\alpha-6sin\alpha}{12sin^3\alpha+108sin^3\alpha}=-\dfrac{3sin\alpha}{120sin^3\alpha}=-\dfrac{1}{40sin^2\alpha}\)

Lời giải:
\(M=\frac{\frac{\sin a}{\cos a}+1}{\frac{\sin a}{\cos a}-1}=\frac{\tan a+1}{\tan a-1}=\frac{\frac{3}{5}+1}{\frac{3}{5}-1}=-4\)
\(N = \frac{\frac{\sin a\cos a}{\cos ^2a}}{\frac{\sin ^2a-\cos ^2a}{\cos ^2a}}=\frac{\frac{\sin a}{\cos a}}{(\frac{\sin a}{\cos a})^2-1}=\frac{\tan a}{\tan ^2a-1}=\frac{\frac{3}{5}}{\frac{3^2}{5^2}-1}=\frac{-15}{16}\)

\(A=cos3a+2cos\left(\pi-3a\right)sin^2\left(\dfrac{\pi}{4}-1,5a\right)\)
\(=cos3a-2cos3a\dfrac{1-cos\left(\dfrac{\pi}{2}-3a\right)}{2}\)
\(=cos3a-cos3a\left(1-sin3a\right)\)
\(=cos3a-cos3a+cos3asin3a=\dfrac{1}{2}sin6a\)
\(=\dfrac{1}{2}sin\left(6\dfrac{5\pi}{6}\right)=\dfrac{1}{2}sin\left(4\pi+\pi\right)=\dfrac{1}{2}sin\pi=0\)
Vì a=\(\dfrac{5\pi}{6}\) nên: \(3a=\dfrac{5\pi}{2}\) => \(\cos3a=0\)
\(\pi-3a=\pi-\dfrac{5\pi}{2}=\dfrac{-3\pi}{2}\)
=> \(\cos\left(\pi-3a\right)=0\)

\(A=\dfrac{4sin^4x-cos^2x\left(1-cos^2x\right)+sin^2x.cos^2x-2cos^2x}{sin^2x}+\dfrac{2}{tan^2x}\)
\(=\dfrac{4sin^4x-sin^2x.cos^2x+sin^2x.cos^2x-2cos^2x}{sin^2x}+2cot^2x\)
\(=4sin^2x-2cot^2x+2cot^2x=4sin^2x\)
\(\Rightarrow\left\{{}\begin{matrix}a=4\\b=2\end{matrix}\right.\)


\(A=\dfrac{3sin\alpha-cos\alpha}{sin\alpha+cos\alpha}=\dfrac{\dfrac{3sin\alpha}{cos\alpha}-1}{\dfrac{sin\alpha}{cos\alpha}-1}=\dfrac{3tan\alpha-1}{tan\alpha-1}\)\(=\dfrac{3\sqrt{2}-1}{\sqrt{2}-1}=5+2\sqrt{2}\).
\(C=\dfrac{\sin a}{\sin^3a+2\cos^3a}=\dfrac{\dfrac{1}{\cos^2a}\cdot\tan a}{\tan^3a+2}=\dfrac{\left(1+\tan^2a\right)\cdot\tan a}{2+\tan^3a}=\dfrac{\left(1+2^2\right)\cdot2}{2+8}=1\)