tại sao 4x^4+36x^2+81-36x^2=(2x^2+9)^2-36x^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(4x^4+36x^2+81-36x^2=\left(4x^4+36x^2+81\right)-36x^2=\left(2x^2+9\right)^2-36x^2=\left(2x^2+9+6x\right)\left(2x^2+9-6x\right)\)
\(4x^4+36x^2+81-36x^2\)
\(=\left(2x-9\right)^2-\left(6x\right)^2=\left(2x^2+9+6x\right)\left(2x^2-6x+9\right)=\left(2x^2+6x+9\right)\left(2x^2-6x+9\right)\)

a) \(x^2+4x+4=\left(x+2\right)^2\)
b) \(\left(x-3\right)\left(x^2+3x+9\right)=x^3-27\)
c) \(x^2-1=\left(x-1\right)\left(x+1\right)\)
d) \(36x^2+36x+9=9\left(2x+1\right)^2\)
Min ra kết quả lun nha bn!
a, (x+2)2
b, x3-33
c, (x-1)(x+1)
d, 9.(2x+1)2

\(A=\sqrt{4x^2-4x+1}+\sqrt{4x^2-36x+81}\)
\(=\sqrt{\left(2x\right)^2-2.2x.1+1^2}+\sqrt{\left(2x\right)^2-2.2x.9+9^2}\)
\(=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(2x-9\right)^2}\)
\(=\left|2x-1\right|+\left|2x-9\right|\)
\(=2x-1+9-2x=8\)

2) \(x^4-5x^2+4\)
\(=x^4-x^2-4x^2+4\)
\(=x^2\left(x^2-1\right)-4\left(x^2-1\right)\)
\(=\left(x^2-1\right)\left(x^2-4\right)\)
\(=\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)\)


a: =>2*căn x+5+căn x+5-1/3*3*căn x+5=4
=>2*căn(x+5)=4
=>căn (x+5)=2
=>x+5=4
=>x=-1
b: =>\(6\sqrt{x-1}-3\sqrt{x-1}-2\sqrt{x-1}+\sqrt{x-1}=16\)
=>2*căn x-1=16
=>x-1=64
=>x=65
c, \(\sqrt{\left(x-3\right)^2}-2\sqrt{\left(x-1\right)^2}+\sqrt{x^2}=0\\ \Leftrightarrow\left|x-3\right|-2\left|x-1\right|+\left|x\right|=0\left(1\right)\)
TH1: \(x\ge3\)
\(\left(1\right)\Rightarrow x-3-2x+2+x=0\\ \Leftrightarrow-1=0\left(loại\right)\)
TH2: \(2\le x< 3\)
\(\left(1\right)\Rightarrow3-x-2x+2+x=0\\ \Leftrightarrow-2x=-5\\ \Leftrightarrow x=\dfrac{5}{2}\left(tm\right)\)
TH3: \(0\le x< 2\)
\(\left(1\right)\Rightarrow3-x+2x-2+x=0\\ \Leftrightarrow2x=1\\ \Leftrightarrow x=\dfrac{1}{2}\left(tm\right)\)
TH4: \(x< 0\)
\(\left(1\right)\Rightarrow3-x+2x-2-x-=0\\ \Leftrightarrow1=0\left(loại\right)\)
Vậy \(x\in\left\{\dfrac{1}{2};\dfrac{5}{2}\right\}\)
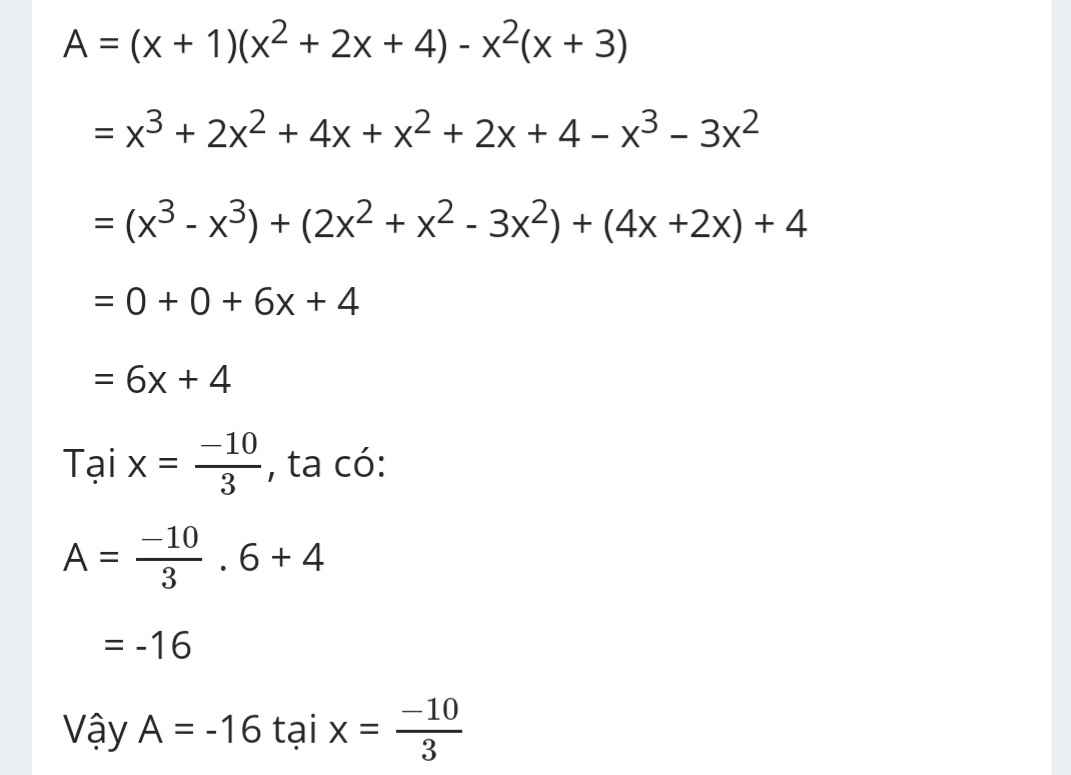

Có: 4x4+36x2+81=(2x2+9)2
<=>4x4+36x2+81-36x2=(2x2+9)2-36x2