Tìm 2 số nguyên x,y biết :
55x + 30y = 3658
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
M
2
1 tháng 2 2022
Lớp 4?
a) \(\dfrac{x+1}{4}=\dfrac{36}{x+1}\)
\(\Rightarrow\left(x+1\right)^2=144\)
\(\Rightarrow\left[{}\begin{matrix}x+1=12\\x+1=-12\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=11\\x=-13\end{matrix}\right.\)
Vậy: \(x\in\left\{11;-13\right\}\)
b) \(\dfrac{x}{7}=\dfrac{55x-4}{28}\)
\(\Rightarrow4x=55x-4\)
\(\Rightarrow-51x=-4\)
\(\Rightarrow x=\dfrac{4}{51}\)
Vậy: \(x=\dfrac{4}{51}\)
BT
1 tháng 2 2022
a) \(\dfrac{x + 1}{4} = \dfrac{36}{x + 1} \)
\(\Rightarrow\) \(( x + 1 )( x + 1 ) = 36 . 4 \)
\(\Rightarrow ( x + 1 )^2 = 144 \)
\(\Rightarrow ( x + 1 )^2 = 12^2 = ( -12 )^2 \)
\(\Rightarrow\) \(x + 1 ∈ \) { \(12 ; -12 \) }
\(\Rightarrow \) \(x \) \(∈ \) { \(11 ; -13 \) }
Vậy \(x ∈ \) { \(11 ; -13 \) }
NN
0
30 tháng 5 2017
Ta có: 46.y là số chẵn với mọi số nguyên y
TH1: Nếu x là số nguyên tố lớn hơn 2 thì suy ra 59.x là số lẻ
suy ra 59.x + 46.y là số lẻ
mà 2004 là số chẵn nên loại trường hợp này.
TH2: Từ TH1 suy ra x phải là số chẵn
Mà trong số nguyên tố thì chỉ có số 2 là số nguyên tố chẵn
Từ đó suy ra x = 2
suy ra y = ( 2004 - 59.2 ) : 46 = 41
Vậy x = 2 ; y = 41
b/ Ta thấy 30.b luôn luôn có tận cùng bằng 0 với mọi b
TH1: a là số nguyện chẵn thì 55.a sẽ có tận cùng là 0
Vậy ta có: 55.a + 30.b = ....0 + .....0 = ....0
mà 3658 tận cùng là 8 nên loại trường hợp này. ( 1 )
TH2: a là số nguyên lẻ thì 55.a sẽ có tận cùng là 5
Vậy ta có: 55.a + 30.b = .....5 + .....0 = .....5
mà 3658 có tận cùng là 8 nên loại trường hợp này. ( 2 )
Từ ( 1 ) và ( 2 ) suy ra không tồn tại a,b để 55.a + 30.b = 3658
Vậy: Không tồn tại a,b thỏa mãn đề bài
Nhớ k cho mình nhé!
HL
1
AH
Akai Haruma
Giáo viên
21 tháng 8 2021
Bạn lưu ý chỉ đăng bài MỘT LẦN thôi chứ không đăng lặp lại gây loãng trang web.
HL
2
AH
Akai Haruma
Giáo viên
21 tháng 8 2021
Lời giải:
a. Ta thấy:
$18x-30y=3(6x-10y)$ chia hết cho $3$ với mọi $x,y$ nguyên, mà $59$ không chia hết cho $3$
Do đó pt $18x-30y=59$ vô nghiệm.
b. $22x-5y=77$
$5y=22x-77=11(2x-7)\vdots 11$
$\Rightarrow y\vdots 11$. Đặt $y=11k$ với $k$ nguyên
$22x-55k=77$
$2x-5k=7$
$2x=5k+7\vdots 2$
$\Rightarrow k$ lẻ. Đặt $k=2t+1$ với $t$ nguyên
$2x=5(2t+1)+7=10t+12$
$x=5t+6$
Vậy $(x,y)=(5t+6, 22t+11)$ với $t$ nguyên
AH
Akai Haruma
Giáo viên
21 tháng 8 2021
c.
$12x+19y=94$
$19y=94-12x\vdots 2\Rightarrow y\vdots 2$
Đặt $y=2k$ với $k$ nguyên. Khi đó:
$12x+38k=94$
$6x+19k=47$
$6k=47-19k=19(2-k)+9$
$\Rightarrow 6k-9\vdots 19$
$\Leftrightarrow 2k-3\vdots 19$
$\Leftrightarrow 2k-22\vdots 19$
$\Leftrightarrow k-11\vdots 19$
$\Rightarrow k=19t+11$ với $t$ nguyên
\(x=\frac{47-19k}{6}=\frac{47-19(19t+11)}{6}=\frac{-162-361t}{6}=-27-\frac{361t}{6}\)
Để $x$ nguyên thì $t\vdots 6$. Khi đó đặt $t=6m$ với $m$ nguyên
Khi đó:
$y=2k=2(19t+11)=2(114m+11)=228m+22$
$x=-27-361m$ với $m$ nguyên bất kỳ.
PT
1
CM
4 tháng 7 2018
Ta có:
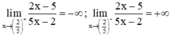
⇒ Đồ thị có tiệm cận đứng là x = 2/5.
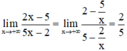
⇒ Đồ thị có tiệm cận ngang là y = 2/5.
Ta có :
\(55x+30y=3658\) \(\left(x,y\in Z\right)\)
\(25x+30x+30y=3658\)
\(25x+30.\left(x+y\right)=3658\)
\(\Rightarrow\)vô lí Vì :
\(25⋮5\)
\(30⋮5\)
\(3658\) \(⋮̸\) \(5\)
\(\Rightarrow\)Không tìm được cặp giá trị \(x,y\) thỏa mãn theo yêu cầu.
Chúc bn học tốt!!
Thanks nha!!!!!!!!