cho a,b,c là 3 cạnh của tam giác. Chứng minh rằng:
a) \(\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}< 2\)
b)\(a^3+b^3+c^3+3abc>ab\left(a+b\right)+bc\left(b+c\right)+ac\left(a+c\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 8 2021
Do a;b;c là độ dài 3 cạnh của tam giác
\(\Rightarrow abc\ge\left(a+b-c\right)\left(b+c-a\right)\left(a+c-b\right)\)
\(\Leftrightarrow4\left(a^3+b^3+c^3\right)+15abc\ge\left(a+b+c\right)^3\)
\(\Leftrightarrow3\left(a^3+b^3+c^3\right)+\dfrac{45}{4}abc\ge\dfrac{3}{4}\left(a+b+c\right)^3\)
\(\Rightarrow3\left(a^3+b^3+c^3\right)+4abc\ge\dfrac{3}{4}\left(a+b+c\right)^3-\dfrac{29}{4}abc\)
Do đó ta chỉ cần chứng minh:
\(\dfrac{3}{4}\left(a+b+c\right)^3-\dfrac{29}{4}abc\ge\dfrac{13}{27}\left(a+b+c\right)^3\)
\(\Leftrightarrow\left(a+b+c\right)^3\ge27abc\) (hiển nhiên đúng theo AM-GM)
2 tháng 8 2022
Câu 1:
a: \(\left(a+b\right)^3-3ab\left(a+b\right)\)
\(=a^3+3a^2b+3ab^2+b^3-3a^2b-3ab^2\)
\(=a^3+b^3\)
b: \(a^3+b^3+c^3-3abc\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 2 2022
Đặt \(a\left(1-b\right)=x;b\left(1-c\right)=y;c\left(1-a\right)=x\)
\(\Rightarrow1-\left(a+b+c\right)+ab+bc+ca=1-a\left(1-b\right)-b\left(1-c\right)-c\left(1-a\right)=1-x-y-z\)
BĐT cần c/m trở thành:
\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\ge\dfrac{3}{1-x-y-z}\)
\(\Leftrightarrow\left(1-x-y-z\right)\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)-3\ge0\)
\(\Leftrightarrow\dfrac{1-x-y-z}{x}+\dfrac{1-x-y-z}{y}+\dfrac{1-x-y-z}{z}-3\ge0\)
\(\Leftrightarrow\dfrac{1-y-z}{x}+\dfrac{1-z-x}{y}+\dfrac{1-x-y}{z}-6\ge0\) (1)
Lại có: \(1-y-z=1-b\left(1-c\right)-c\left(1-a\right)=1-b-c+bc+ca=\left(1-b\right)\left(1-c\right)+ca\)
Nên (1) tương đương:
\(\dfrac{\left(1-b\right)\left(1-c\right)+ca}{a\left(1-b\right)}+\dfrac{\left(1-a\right)\left(1-c\right)+ab}{b\left(1-c\right)}+\dfrac{\left(1-a\right)\left(1-b\right)+bc}{c\left(1-a\right)}-6\ge0\)
\(\Leftrightarrow\dfrac{1-c}{a}+\dfrac{c}{1-b}+\dfrac{1-a}{b}+\dfrac{a}{1-c}+\dfrac{1-b}{c}+\dfrac{b}{1-a}\ge6\)
BĐT trên hiển nhiên đúng theo AM-GM do:
\(\dfrac{1-c}{a}+\dfrac{c}{1-b}+\dfrac{1-a}{b}+\dfrac{a}{1-c}+\dfrac{1-b}{c}+\dfrac{b}{1-a}\ge6\sqrt[6]{\dfrac{abc\left(1-a\right)\left(1-b\right)\left(1-c\right)}{abc\left(1-a\right)\left(1-b\right)\left(1-c\right)}}=6\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{2}\)
19 tháng 2 2022
Cám ơn bài giải của thầy Lâm ạ!
Và từ bài bất đăng thức này, đã được chế thành bài toán hình học trong 1 kì thi học sinh giỏi toán cấp tỉnh thầy ạ!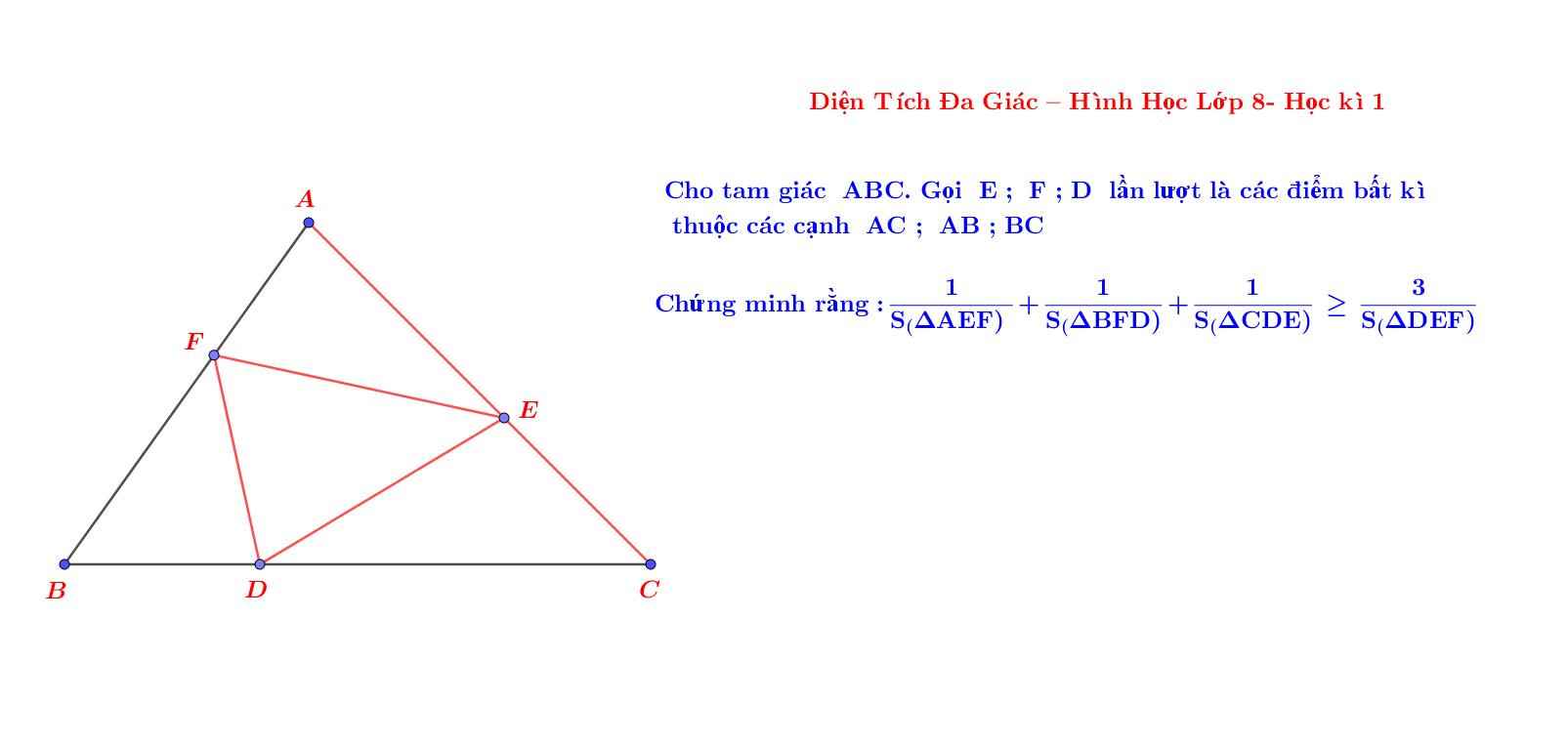
a)\(\dfrac{a}{b+c}< \dfrac{2a}{a+b+c}\) tương tự ta có ĐPCM
b)chính nó là BĐT Schur bậc 3 cách c/m nhiều vô kể
b ơi giải đầy đủ giúp m đc ko?
còn câu b) thì c/m giúp m cách nào đó nha
m mới học phần này nên chưa chắc kiến thức lắm nên giúp m nha