Cho đoạn thẳng AB, 2 đường thẳng d và d' lần lượt vuông góc với AB tại A và B. Gọi O là trung điểm của AB. Lấy C, D thuộc d và d' sao cho góc COD bằng 90 độ. Chứng minh CD là tiếp tuyến của đường tròn đường kính AB.
(Gợi ý: Vẽ OH vuông góc với CD, rồi tìm cách chứng minh OA = OH).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

17 tháng 9 2023
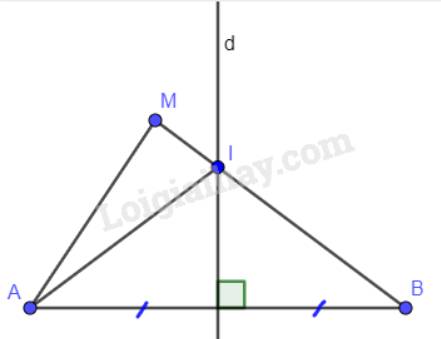
a) Ta có: Đường thẳng d là đường trung trực của đoạn thẳng AB. Mà điểm I thuộc đường thẳng d nên suy ra: IA = IB. (Một điểm thuộc đường trung trực thì cách đều hai đầu mút).
Ta có: \(MB = MI + IB\) mà IA = IB nên \(MB = MI + IA = AI + IM\).
b) Xét tam giác AMI có: \(MA < AI + IM\)(Tổng hai cạnh bất kì trong một tam giác luôn lớn hơn độ dài cạnh còn lại) mà \(MB = AI + IM\).
Vậy \(MA < MB\).

KN
11 tháng 4 2023
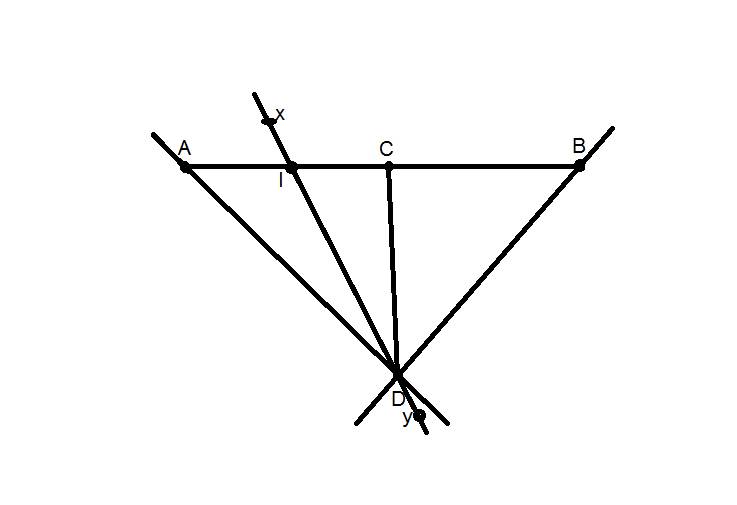
a) các tia đối nhau có gốc là I:
-AI với IC
-xI với Iy
-xI với ID
các tia trùng nhau có gốc I là:
- IC trùng với IB
- ID trùng với Iy
b) các góc đỉnh D là:
-AID,ADx, xDC, IDC, CDB, ADC,xDB,IDB, ADB

EC
21 tháng 8 2016
Cái này mk chưa học bn à mk xin lỗi nhé có thể bn nhờ các thầy cô giáo

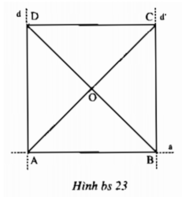
hình ông tự vẽ nha
kẻ OH vuông góc với CD
Kẻ OK là trung tuyến của tam giác CMD
xét tam giác CMD vuông tại M có
MK=CK = 1/2 CD (MK là tiếp tuyến )
=> CKM là tam giác cân, cân tại K
=> góc MKC = góc KMC
AC vuông góc với AB
BD vuông góc với AB
=> AC // BD
=>ACBD là hình thang
AM = MB
CK=KD
=>MK là đường trung bình
=> MK // CA
=> góc ACM = góc KMC
mà góc KMC = góc KCM (cmt)
=> góc ACM = góc KCM
=> góc HMC= góc CMA (cùng phụ 2 góc đó)
xét tam giác MAC và tam giác MHC có:
góc CAM = góc CHM = 90 độ
góc ACM= góc HCM ( cmt)
=> góc HMC= góc CMA
=> tam giác MAC = tam giác MHC
=> HM = AM mà HM vuông CD => ĐPCM
bài có ít sai sót ông xem thử nha