Cho tam giác ABC có B=500 và C=200 ,đường cao AH.Tia phân giác góc AHC cắt AC tại D.Vẽ tia Ax là tia đối tia AB.Chứng minh rằng điểm D nằm trên tia phân giác của góc ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
WJ
15 tháng 11 2015
Xét \(\Delta ABEvà\Delta ACKtacó:\)
AB=CK (1)
góc ABE= góc ACK (cùng bằng bù nhau với góc ACB) (2)
BE=DC (3)
Tứ (1), (2), (3) \(\Rightarrow\Delta ABE=\Delta ACK\left(c-g-c\right)\)
\(\Rightarrow EA=AK\)(cặp cạnh tương ứng)
7 tháng 2 2023
Bài 2:
Kẻ OF//BC(F thuộc AC)
=>OF//DE//BC
DE//BC
=>góc DEA=góc ACB
=>góc DEO=1/2*góc ACB
ED//OF
=>góc DEA=góc CFD và góc DEO=góc EOF
=>góc EOF=1/2*góc ACB
=>góc DEO=góc EOF
OF//BC
=>góc FOB=góc OBC=1/2góc ABC
góc BOE=góc BOF+góc EOF
=1/2(góc ABC+góc ACB)
1 tháng 2 2022
Bài 3:
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra:AC//BD và AC=BD
c: Xét ΔABC và ΔDCB có
AB=DC
\(\widehat{ABC}=\widehat{DCB}\)
BC chung
Do đó: ΔABC=ΔDCB
Suy ra: \(\widehat{BAC}=\widehat{CDB}=90^0\)
CM
1 tháng 8 2019
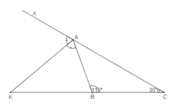
+) Hai góc ∠ABK và ∠ABC là hai góc kề bù nên:
∠ABK = 180° - ∠ABC = 180° - 110° = 70° (1)
+) Góc Bax là góc ngoài tam giác tại đỉnh A của tam giác ACK nên:
∠BAx = 110° + 30° = 140° ( tính chất góc ngoài tam giác).
+) Do AK là tia phân giác của góc BAx nên:
∠BAK = ∠BAx : 2 = 140° : 2 = 70°. (2)
Từ (1) và (2) suy ra tam giác KAB có hai góc bằng nhau.
DT
27 tháng 4 2019
đề bài thiếu bn ơi, ko cho H là j mà câu a) lại bắt c/m góc ADH=góc ADB à
