Giúp mình câu 7 phần b với ạ!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
2
TM
6 tháng 4 2023
Bài III.2b.
Phương trình hoành độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\) : \(x^2=\left(m+1\right)x-m-4\)
hay : \(x^2-\left(m+1\right)x+m+4=0\left(I\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm nên phương trình \(\left(I\right)\) sẽ có hai nghiệm phân biệt. Do đó, phương trình \(\left(I\right)\) phải có :
\(\Delta=b^2-4ac=\left[-\left(m+1\right)\right]^2-4.1.\left(m+4\right)\)
\(=m^2+2m+1-4m-16\)
\(=m^2-2m-15>0\).
\(\Rightarrow m< -3\) hoặc \(m>5\).
Theo đề bài : \(\sqrt{x_1}+\sqrt{x_2}=2\sqrt{3}\)
\(\Rightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=\left(2\sqrt{3}\right)^2=12\)
\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=12\left(II\right)\)
Do phương trình \(\left(I\right)\) có hai nghiệm khi \(m< -3\) hoặc \(m>5\) nên theo định lí Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m+1\right)}{1}=m+1\\x_1x_2=\dfrac{c}{a}=\dfrac{m+4}{1}=m+4\end{matrix}\right.\).
Thay vào \(\left(II\right)\) ta được : \(m+1+2\sqrt{m+4}=12\)
Đặt \(t=\sqrt{m+4}\left(t\ge0\right)\), viết lại phương trình trên thành : \(t^2-3+2t=12\)
\(\Leftrightarrow t^2+2t-15=0\left(III\right)\).
Phương trình \(\left(III\right)\) có : \(\Delta'=b'^2-ac=1^2-1.\left(-15\right)=16>0\).
Suy ra, \(\left(III\right)\) có hai nghiệm phân biệt :
\(\left\{{}\begin{matrix}t_1=\dfrac{-b'+\sqrt{\Delta'}}{a}=\dfrac{-1+\sqrt{16}}{1}=3\left(t/m\right)\\t_2=\dfrac{-b'-\sqrt{\Delta'}}{a}=\dfrac{-1-\sqrt{16}}{1}=-5\left(ktm\right)\end{matrix}\right.\)
Suy ra được : \(\sqrt{m+4}=3\Rightarrow m=5\left(ktm\right)\).
Vậy : Không có giá trị m thỏa mãn đề bài.
TM
6 tháng 4 2023
Bài IV.b.
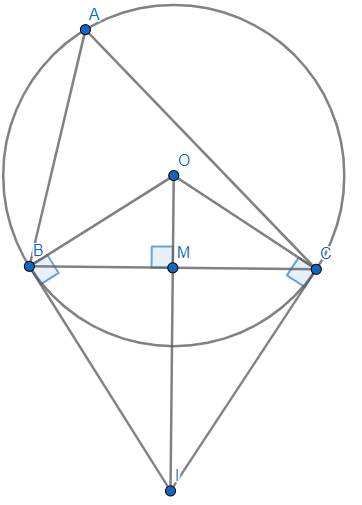
Chứng minh : Ta có : \(OB=OC=R\) nên \(O\) nằm trên đường trung trực \(d\) của \(BC\).
Theo tính chất hai tiếp tuyến cắt nhau thì \(IB=IC\), suy ra \(I\in d\).
Suy ra được \(OI\) là một phần của đường trung trực \(d\) của \(BC\) \(\Rightarrow OI\perp BC\) tại \(M\) và \(MB=MC\).
Xét \(\Delta OBI\) vuông tại \(B\) có : \(MB^2=OM.OI\).
Lại có : \(BC=MB+MC=2MB\)
\(\Rightarrow BC^2=4MB^2=4OM.OI\left(đpcm\right).\)
Tính diện tích hình quạt tròn
Ta có : \(\hat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\Rightarrow sđ\stackrel\frown{BC}=2.\hat{BAC}=2.70^o=140^o\) (góc nội tiếp).
\(\Rightarrow S=\dfrac{\pi R^2n}{360}=\dfrac{\pi R^2.140^o}{360}=\dfrac{7}{18}\pi R^2\left(đvdt\right)\)
3 tháng 2 2022
\(A=\dfrac{2x-4\sqrt{x}+2-\left(2\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{x-4}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
\(=\dfrac{2x-4\sqrt{x}+2-2x+4\sqrt{x}+\sqrt{x}-2}{\sqrt{x}+2}\cdot\dfrac{1}{\sqrt{x}}\)
\(=\dfrac{1}{\sqrt{x}+2}\)
30 tháng 3 2021
Mùa hạ qua đi,mùa thu lại về tiếng trống ngày khai trường lại rộn rã vang lên.Thế là tâm trạng của mỗi người hs lại vừa mừng vừa lo.Ôi ! Vui mừng biết bao khi được gặp lại bạn bè thầy cô giáo. Lo lắng biết bao khi chưa biết thầy cô giáo nào chủ nhiệm.Ngày qua ngày, chúng em cũng được biết.Thế mà giờ đây cũng đã trôi qua một học kì,em yêu quý biết bao những ngày tháng ấy
Câu rút gọn: Vui mừng biết bao khi được gặp lại bạn bè thầy cô giáo. Lo lắng biết bao khi chưa biết thầy cô giáo nào chủ nhiệm
30 tháng 3 2021
Đã qua những ngày Tết cổ truyền, con lại bước chân lên tàu, và đi, đi đến một miền đất xa xôi mà con đã chọn để học tập. Con đi xa mẹ, xa gia đình, xa bạn bè và xa quê hương. Ôi! Hai tiếng quê hương! Nhớ quê! Con chỉ biết khóc, con thấy đâu đây vị ngọt, ngọt ngài của nước mắt, chính quê hương đã ban cho con những giọt nước mắt ngọt ngào đó. Ngày mai, con sẽ xa nơi này, đến phương trời kia, không phải là phương trời quen thuộc như mỗi lần con nằm dưới bãi cỏ và ngắm nhìn. Đi! Đi thật xa! Gặp những con người mới của xứ lạ.Con sẽ nhớ... . Dưới bầu trời xa lạ ấy, quê hương con nằm ở đây, trong tim này của con.
TA
1
26 tháng 12 2021
\(n_{Fe}=\dfrac{16,8}{56}=0,3\left(mol\right)\)
PTHH: Fe + 2HCl --> FeCl2 + H2
____0,3---->0,6
=> mHCl = 0,6.36,5 = 21,9(g)
YH
1
Y
11 tháng 10 2023
Câu 2 :
Ta có : \(AH=HB.HC\) (Hệ thức lượng trong \(\Delta ABC\))
\(\Rightarrow AH=3.9=27\left(cm\right)\)
Xét \(\Delta ABH\perp\) tại H có :
\(AB^2=HB^2+AH^2\) \(\left(d/lPytago\right)\)
\(\Rightarrow AB^2=9^2+27^2=810\)
\(\Rightarrow AB=\sqrt{810}=9\sqrt{10}\left(cm\right)\)
Vậy \(AB=9\sqrt{10}cm\)