Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có M ∈ O x nên M(x;O) và M A → = − 4 − x ; 0 M B → = − 5 − x ; 0 M C → = 3 − x ; 0 ⇒ M A → + M B → + M C → = − 6 − 3 x ; 0 .
Do M A → + M B → + M C → = 0 → nên − 6 − 3 x = 0 ⇔ x = − 2 ⇒ M − 2 ; 0 .
Chọn A.

a, \(\overrightarrow{BA}=\left(0-4;-2-1\right)\)
=\(\left(-4;-3\right)\)

Lời giải:
$I$ là trung điểm $AB$ nên:
\(\left\{\begin{matrix}
\frac{x_A+x_B}{2}=x_I\\
\frac{y_A+y_B}{2}=y_I\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x_B=2x_I-x_A\\
y_B=2y_I-y_A\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x_B=2.0-1=-1\\ y_B=2(-2)-0=-4\end{matrix}\right.\)
Vậy $B(-1,-4)$

VTCP là (-1;2)
Phương trình chính tắc là: \(\dfrac{x-1}{-1}=\dfrac{y-0}{2}=\dfrac{y}{2}\)

Lời giải:
Tọa độ trung điểm $M$ của $AB$ là:
\(\left(\frac{x_A+x_B}{2}; \frac{y_A+y_B}{2}\right)=\left(\frac{2+0}{2}; \frac{5+(-7)}{2}\right)=(1;-1)\)

a)
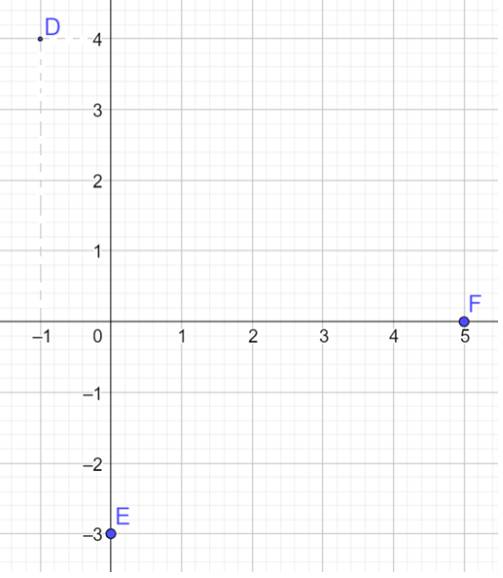
b) Vì tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ của điểm M (với mọi M) nên ta có:
\(\overrightarrow {OD} = \left( { - 1;4} \right),\overrightarrow {OE} = \left( {0; - 3} \right),\overrightarrow {OF} = \left( {5;0} \right)\)
c)
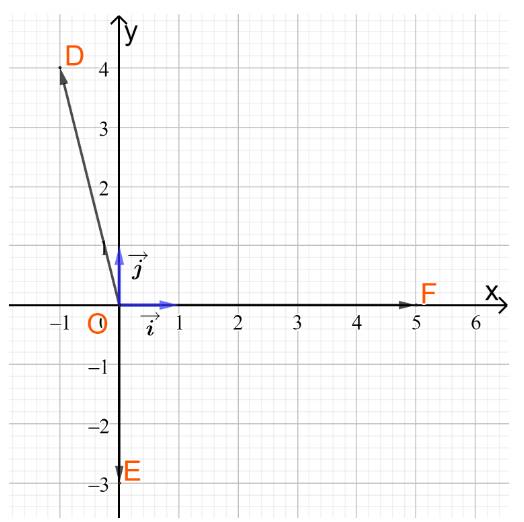
Từ hình vẽ ta có tọa độ của hai vectơ và \(\overrightarrow j \)là
và \(\overrightarrow j = (0;1)\)

a)
Ta có: \(\overrightarrow {AB} = \left( {2 - 1;4 - 3} \right) = \left( {1;1} \right),\;\overrightarrow {AC} = \left( { - 3 - 1;2 - 3} \right) = \left( { - 4; - 1} \right)\)
Hai vectơ này không cùng phương (vì \(\frac{1}{{ - 4}} \ne \frac{1}{{ - 1}}\)).
Do đó các điểm A, B, C không cùng nằm trên một đường thẳng.
Vậy A, B, C là ba đỉnh của một tam giác.
b) Trung điểm M của đoạn thẳng AB có tọa độ là \(\left( {\frac{{1 + 2}}{2};\frac{{3 + 4}}{2}} \right) = \left( {\frac{3}{2};\frac{7}{2}} \right)\)
c) Trọng tâm G của tam giác ABC có tọa độ là \(\left( {\frac{{1 + 2 + \left( { - 3} \right)}}{3};\frac{{3 + 4 + 2}}{3}} \right) = \left( {0;3} \right)\)
d) Để O(0; 0) là trọng tâm của tam giác ABD thì \(\left( {0;0} \right) = \left( {\frac{{{x_A} + {x_B} + {x_D}}}{3};\frac{{{y_A} + {y_B} + {y_D}}}{3}} \right)\)
\( \Leftrightarrow \left( {0;0} \right) = \left( {\frac{{1 + 2 + x}}{3};\frac{{3 + 4 + y}}{3}} \right)\)
\(\begin{array}{l} \Leftrightarrow \left( {0;0} \right) = \left( {1 + 2 + x;3 + 4 + y} \right)\\ \Leftrightarrow \left( {0;0} \right) = \left( {x + 3;y + 7} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}0 = x + 3\\0 = y + 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = - 7\end{array} \right.\end{array}\)
Vậy tọa độ điểm D là (-3; -7).

Gọi M là trung điểm AB
\(\Rightarrow\left\{{}\begin{matrix}x_M=\frac{x_A+x_B}{2}=\frac{1+0}{2}=\frac{1}{2}\\y_M=\frac{y_A+y_B}{2}=\frac{0-2}{2}=-1\end{matrix}\right.\)
\(\Rightarrow M\left(\frac{1}{2};-1\right)\)
Gọi I là TĐ AB
\(\Rightarrow\left\{{}\begin{matrix}x_I=\frac{x_A+x_B}{2}\\y_I=\frac{y_A+y_B}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_I=\frac{1+0}{2}\\y_I=\frac{0-2}{2}\end{matrix}\right.\Rightarrow I\left(\frac{1}{2};-1\right)\)
x y 0 C A B H M Gọi điểm H(1;0) , M(0;1)
\(S_{MOHC}\) : \(1\cdot1=1\)
\(S_{CHB}=S_{CMA}=\dfrac{1}{2}\cdot5\cdot1=\dfrac{5}{2}\)
\(S_{AOB}=\dfrac{1}{2}\cdot6\cdot6=18\)
\(\Rightarrow S_{ABC}=S_{AOB}-S_{MOHC}-S_{CHB}-S_{CMA}=18-1-\dfrac{5}{2}-\dfrac{5}{2}=12\)Vậy diện tích tam giác ABC bằng 12
v17 nhé tặng bn =12 tìm cách giải đi, k làm dc mk chỉ