Có bao nhiêu cặp số nguyên (x;y) thỏa mãn đẳng thức
3xy+x-y=1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(n_{Na}=\dfrac{11,5}{23}=0,5(mol)\)
Số nguyên tử Na: \(0,5.6.10^{23}=3.10^{23}\)
\(\Rightarrow n_{Fe}=0,5(mol)\\ \Rightarrow m_{Fe}=0,5.56=28(g)\)

Đáp án C
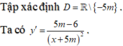
Để hàm số nghịch biến trên khoảng ( 10 ; + ∞ ) thì

uses crt;
var st:string;
dem,i,d:integer;
begin
clrscr;
write('st='); readln(st);
d:=length(st);dem:=0;
for i:=1 to d do
if st[i] in['0'..'9'] then inc(dem);
writeln(dem);
readln;
end.

Chọn C
Hàm số f(x) =
2
x
2
+
m
x
+
2
3
2
xác định với mọi
x
∈
ℝ
![]()
![]()
Vì m nguyên nên ![]()
Vậy có tất cả 7 giá trị m thỏa mãn điều kiện đề bài.
\(3xy+x-y=1\)
\(\Leftrightarrow3xy+x=y+1\)
\(\Leftrightarrow x\left(3y+1\right)=y+1\)
\(\Rightarrow y+1⋮3y+1\)
\(\Rightarrow3y+3⋮3y+1\)
\(\Rightarrow\left(3y+2\right)+2⋮3y+1\)
\(\Rightarrow2⋮3y+1\)
\(\Rightarrow3y+1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
Với:
\(3y+1=-2\Rightarrow y=-1\Leftrightarrow x=0\)
\(3y+1=-1\Rightarrow y=\frac{-2}{3}\) (loại vì \(y\notin Z\))
\(3y+1=1\Rightarrow y=0\Leftrightarrow x=1\)
\(3y+1=2\Rightarrow y=\frac{1}{3}\) (loại vì \(y\notin Z\))
Vậy có \(2\) cặp số nguyên \(\left(x;y\right)\) là \(\left(0;-1\right),\left(1;0\right)\)