Chứng minh f'(x)>0 với mọi x\(\in\)R biết f(x)=\(\dfrac{2}{3}x^9-x^6+2x^3-3x^2+6x-1\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


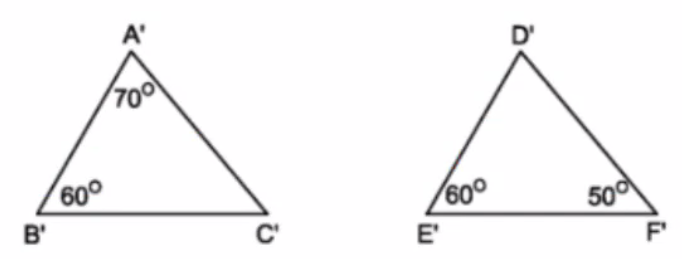
Xét \(\Delta D'E'F':\)
\(\widehat{D'}+\widehat{E'}+\widehat{F'}=180^o\) (Tổng 3 góc trong tam giác).
\(\Rightarrow\widehat{D'}+60^o+50^o=180^o.\\ \Rightarrow\widehat{D'}=70^o.\\ \Rightarrow\widehat{D'}=\widehat{A'}\left(=70^o\right).\)
Xét \(\Delta A'B'C'\) và \(\Delta D'E'F':\)
\(\widehat{A'}=\widehat{D'}\left(cmt\right).\)
\(\widehat{B'}=\widehat{E'}\left(=60^o\right).\)
\(\Rightarrow\) \(\Delta A'B'C'\sim\) \(\Delta D'E'F'\left(g-g\right).\)
\(\Rightarrow\dfrac{B'C'}{E'F'}=\dfrac{A'C'}{D'F'}\) (2 cạnh tương ứng).
\(\Rightarrow B'C'.D'F'=A'C'.E'F'.\)

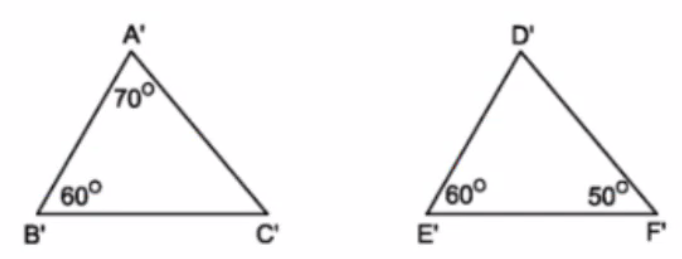
a: \(\widehat{C'}=180^0-60^0-70^0=50^0\)
Xét ΔA'B'C' và ΔD'E'F' có
\(\widehat{B'}=\widehat{E'};\widehat{C'}=\widehat{F'}\)
Do đó:ΔA'B'C'\(\sim\)ΔD'E'F'
b: Ta có: ΔA'B'C'\(\sim\)ΔD'E'F'
nên A'C'/D'F'=B'C'/E'F'
hay \(A'C'\cdot E'F'=B'C'\cdot D'F'\)

a: Xét ΔABC có
D là trung điểm cuả AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BF và DE=BF
hay BDEF là hình bình hành
b: Xét ΔABC có
F là trung điểm của BC
E là trung điểm của AC
Do đó: FE là đường trung bình của ΔABC
Suy ra: FE//AD và FE=AD
hay ADFE là hình bình hành
\(f'=6x^8-6x^5+6x+6=6\left(x^8-x^5+x+1\right)\)
\(\left[{}\begin{matrix}\left|x\right|\le1\Rightarrow\left|x^5-x\right|\le\left|x\right|\le1\Rightarrow1-x^5-x\ge0\\\left|x\right|\ge1\Rightarrow\left|x^5\right|\le x^8\Rightarrow\left\{{}\begin{matrix}x^8-x^5>0\\x^2-x>0\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow f'\left(x\right)>0\forall x\)
lập luận 1 noi ,kết luận 1 ngã...ketluan:ngu vai.