Tìm số tự nhiên x thỏa mãn:( 3.x+1 ) 3 = 343
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 9 2021
(2x + 1)3 = 343
=> (2x + 1)3 = 73
=> 2x + 1 = 7
=> 2x = 6
=> x = 3
︵✰ŦO꙰rᎬv̤̈єŕ๑A͙ʟ0ɲéȸ
Forever Alone
28 tháng 9 2021
(2x + 1)3 = 73
\(\Rightarrow\)2x + 1 = 7
2x = 7 - 1
2x = 6
x = 6 : 2
x = 3
TH
5
TM
14 tháng 8 2020
(2x + 1)3 = 343
=> (2x + 1)3 = 73
=> 2x + 1 = 7
=> 2x = 6
=> x = 3
KN
14 tháng 8 2020
\(\left(2x+1\right)^3=343\)
\(\Leftrightarrow\left(2x+1\right)^3=7^3\)
\(\Leftrightarrow2x+1=7\)
\(\Leftrightarrow2x=6\)
\(\Leftrightarrow x=3\)
PT
1
NT
2
15 tháng 9 2023
Ước nguyên dương của 6=(1,2,3,6)
Với x-1=1 và y-3=6
=>x=2,y=9(T/m)
Với x-1=6,y-3=1
=>x=7,y=4(T/m)
Với x-1=2,y-3=3
=>x=3,y=6(T/m)
Với x-1=3,y-3=2
=>x=4,y=5(T/m)
Vậy các cặp số tự nhiên x,y thỏa mãn là (2,9;7,4;3,6;4,5)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
16 tháng 9 2023
\(\Rightarrow\left(x-1\right),\left(y-3\right)\inƯ\left(6\right)=\left\{1;2;3;6\right\}\)
Lập bảng:
| x-1 | 1 | 2 | 3 | 6 |
| x | 2 | 3 | 4 | 7 |
| y-3 | 6 | 3 | 2 | 1 |
| y | 9 | 6 | 5 | 4 |
=> Tất cả các cặp thoả mãn. Vậy các cặp (x;y) thoả mãn là: (2;9); (3;6); (4;5); (7;4)
MG
2
HP
8 tháng 1 2016
\(\frac{3}{x+3}>\frac{1}{x}>\frac{4}{x+7}=>\frac{3.4}{4.\left(x+3\right)}>\frac{12}{12x}>\frac{4.3}{3.\left(x+7\right)}=>\frac{12}{4x+12}>\frac{12}{12x}>\frac{12}{3x+21}\)
=>4x+12<12x<3x+21
x là stn =>x=2
AH
Akai Haruma
Giáo viên
22 tháng 11 2021
Lời giải:
Nếu $y=0$ thì $3^x=2^y+1=2$ (vô lý)
Nếu $y=1$ thì $3^x=2^y+1=3\Rightarrow x=1$
Nếu $y\geq 2$ thì $3^x=2^y+1\equiv 1\pmod 4$
Mà $3^x\equiv (-1)^x\pmod 4$
$\Rightarrow (-1)^x\equiv 1\pmod 4$
$\Rightarrow x$ chẵn. Đặt $x=2k$ thì:
$2^y=3^x-1=3^{2k}-1=(3^k-1)(3^k+1)$
$\Rightarrow$ tồn tại $n>m >0$ tự nhiên sao cho $3^k-1=2^m; 3^k+1=2^n$ với $m+n=y$
$\Rightarrow 2^n-2^m=2$.
$\Rightarrow 2^{n-1}-2^{m-1}=1$
$\Rightarrow 2^{m-1}$ lẻ
$\Rightarrow m=1\Rightarrow n=2$
$\Rightarrow y=m+n=3$
$3^x=1+2^y=1+2^3=9\Rightarrow x=2$
Vậy $(x,y)=(2,3), (1,1)$
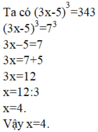
( 3. x + 1 )3 = 343
( 3. x + 1 )3 = 73
=> 3x + 1 = 7
=> 3x = 6
=> x = 2