cho \(x^3\)+\(y^3\)+\(z^3\)=3 .CMR \(x^5+y^5+z^5\ge3\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có:
\(x+y+z=0\)
\(\Rightarrow x+y=-z\)
\(\Rightarrow\left(x+y\right)^3=\left(-z\right)^3\)
\(\Rightarrow x^3+y^3+3xy\left(x+y\right)=-z^3\)
\(\Rightarrow x^3+y^3+z^3=3xyz\)
\(\Rightarrow5\left(x^3+y^3+z^3\right)\left(x^2+y^2+z^2\right)=15xyz\left(x^2+y^2+z^2\right)\)
Mặt khác:
\(x+y+z=0\)
\(\Rightarrow x+y=-z\)
\(\Rightarrow x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5=-z^5\)
\(\Rightarrow x^5+y^5+z^5+5xy\left(x^3+2x^2y+2xy^2+y^3\right)=0\)
\(\Rightarrow x^5+y^5+z^5+\left[\left(x+y\right)\left(x^2-xy+y^2\right)+2xy\left(x+y\right)\right]=0\)
\(\Rightarrow x^5+y^5+z^5+\left(x+y\right)\left(x^2+xy+y^2\right)=0\)
\(\Rightarrow x^5+y^5+z^5-5xyz\left(x^2+xy+y^2\right)=0\)
\(\Rightarrow2\left(x^5+y^5+z^5\right)-5xyz\left[\left(x^2+2xy+y^2\right)+x^2+y^2\right]=0\)
\(\Rightarrow2\left(x^5+y^5+z^5\right)=5xyz\left(x^2+y^2+z^2\right)\)
Khi đó:\(6\left(x^5+y^5+z^5\right)=15xyz\left(x^2+y^2+z^2\right)=VT\)
\(\Rightarrowđpcm\)

\(\frac{x}{1998}=\frac{y}{1999}=\frac{z}{2000}=t=\frac{x-z}{1998-2000}=\frac{x-y}{1998-1999}=\frac{y-z}{1999-2000}.\)
Hay: \(\frac{x-z}{-2}=\frac{x-y}{-1}=\frac{y-z}{-1}\Rightarrow x-z=2\left(x-y\right)=2\left(y-z\right)\)(1)
a) \(\left(x-z\right)^3=\left(x-z\right)^2\left(x-z\right)=\left(2\left(x-y\right)\right)^2\left(2\left(y-z\right)\right)\)
\(\Leftrightarrow\left(x-z\right)^3=8\left(x-y\right)^2\left(y-z\right)\)ĐPCM a)
b) Từ (1) => x + z = 2y
Để \(2\left(x+y\right)=5\left(y+z\right)=3\left(z+x\right)\Rightarrow\frac{x+y}{\frac{1}{2}}=\frac{y+z}{\frac{1}{5}}=\frac{z+x}{\frac{1}{3}}\)
Từ \(\Rightarrow\frac{x+y}{\frac{1}{2}}=\frac{y+z}{\frac{1}{5}}=\frac{x+y+y+z}{\frac{1}{2}+\frac{1}{5}}=\frac{4y}{\frac{7}{10}}=\frac{2y}{\frac{1}{3}}\)
=>y=0 =>x=0 => z=0 Suy ra hệ thức: x-y/4=y-z/5 luôn đúng. ĐPCM

\(\dfrac{\sqrt{1+x^3+y^3}}{xy}>=\sqrt{\dfrac{3}{xy}}\)
\(\dfrac{\sqrt{1+y^3+z^3}}{yz}>=\sqrt{\dfrac{3}{yz}}\)
\(\dfrac{\sqrt{1+z^3+x^3}}{xz}>=\sqrt{\dfrac{3}{xz}}\)
=>\(VT>=\sqrt{3}\left(\dfrac{1}{\sqrt{xy}}+\dfrac{1}{\sqrt{yz}}+\dfrac{1}{\sqrt{xz}}\right)=3\sqrt{3}\)

\(VT=x^3+y^3+z^3=\frac{x^4}{x}+\frac{y^4}{y}+\frac{z^4}{z}\ge\frac{\left(x^2+y^2+z^2\right)^2}{x+y+z}\ge\frac{\left(x^2+y^2+z^2\right)^2}{\sqrt{3\left(x^2+y^2+z^2\right)}}=3\)
Vậy BĐT được chứng minh . Dấu = xảy ra khi \(a=b=c=1\)

Có đúng không...? Tớ cũng đang mắc bài này...?
Ta có: \(x^3+y^3+z^3\ge x^2+y^2+z^2\forall x,y,z>0\)
Dấu "=" xảy ra khi x=y=z=1
Mà \(x^2+y^2+z^2=3\)
\(\Rightarrow x^3+y^3+z^3\ge3\)
\(\Rightarrowđpcm\)
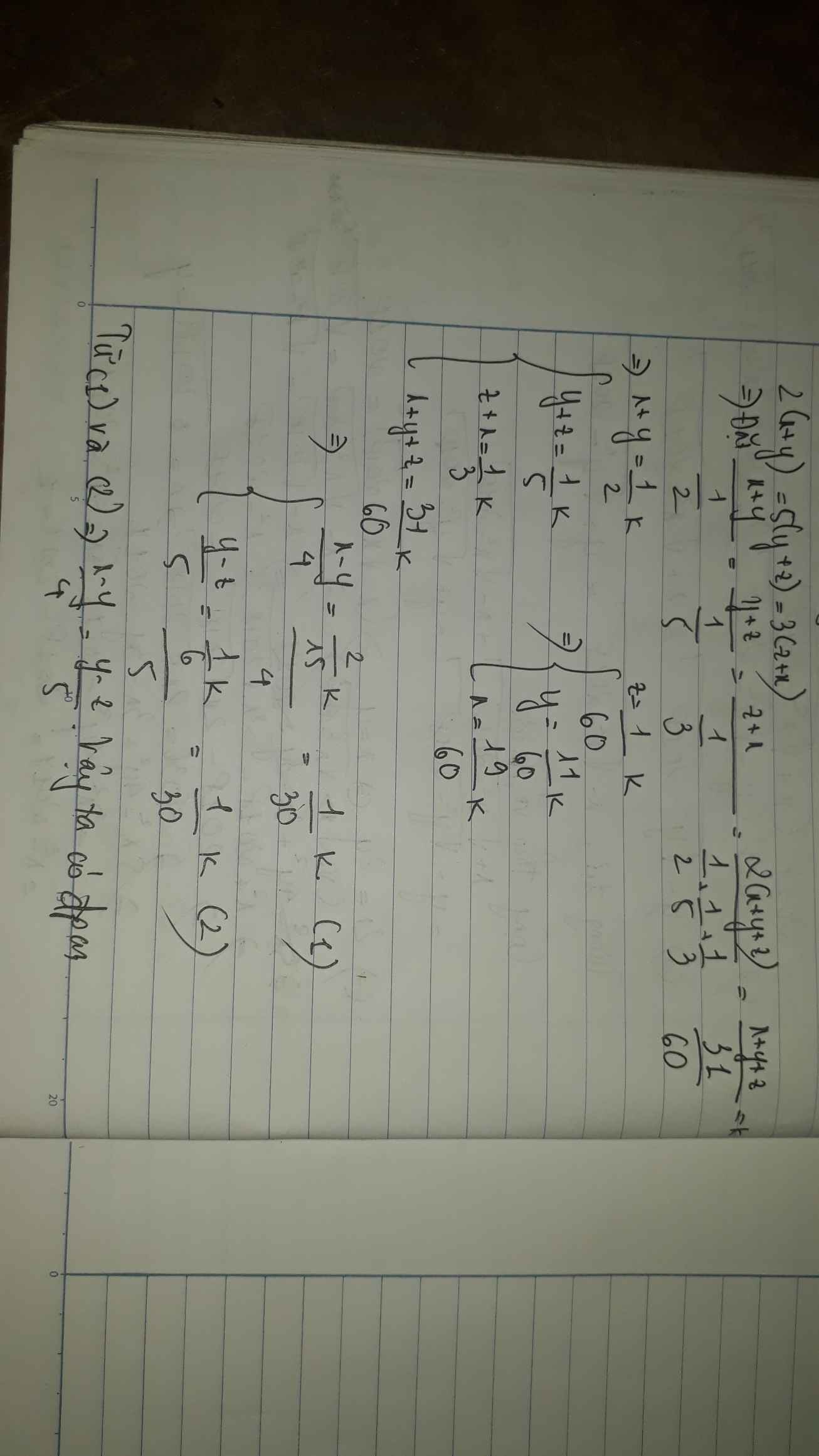
kmjkjpjpi
mình quên ĐK là x,y,z dương