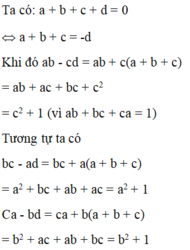cho a2+b2=c2+d2=2010 và ad+bc=0. tính ab+cd
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 7 2021
\(ac+bd=0\)
\(=\) \(abc^2+abd^2+cda^2+cdb^2\)
\(=\) \(ac\left(bc+ad\right)+bd\left(ad+bc\right)\)
\(=\) \(\left(bc+ad\right)\left(ac+bd\right)=0\) \([\) vì ac+bd = 0 \(]\)
12 tháng 5 2022
\(\left(ad+bc\right)\left(a^2d^2+b^2c^2\right)=0\)
\(\Rightarrow a^3d^3+adb^2c^2+bca^2d^2+b^3c^3=0\)
\(\Rightarrow a^3d^3+abcd\left(bc+ad\right)+b^3c^3=0\)
\(\Rightarrow a^3d^3+abcd.0+b^3c^3=0\)
\(\Rightarrow a^3d^3+b^3c^3=0\)
BD
3
27 tháng 1 2022
\(1,\left(ac+bd\right)^2+\left(ad-bc\right)^2\\ =a^2c^2+2abcd+b^2d^2+a^2d^2-2abcd+b^2c^2\\ =a^2c^2+b^2d^2+a^2d^2+b^2c^2\\ =\left(a^2c^2+a^2d^2\right)+\left(b^2d^2+b^2c^2\right)\\ =a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)\\ =\left(a^2+b^2\right)\left(c^2+d^2\right)\)
2, \(\left(a^2+b^2\right)\left(c^2+d^2\right)\ge\left(ac+bd\right)^2\)
\(\Leftrightarrow a^2c^2+b^2c^2+a^2d^2+b^2d^2\ge a^2c^2+2abcd+b^2d^2\)
\(\Leftrightarrow b^2c^2-2abcd+a^2d^2\ge0\)
\(\Leftrightarrow\left(bc-ad\right)^2\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow bc=ad\Leftrightarrow\dfrac{a}{b}=\dfrac{c}{d}\)
TQ
27 tháng 1 2022
\(1\)/
⇔ \(\left(ac\right)^2+2abcd+\left(bd\right)^2+\left(ad\right)^2-2abcd+\left(bc\right)^2=\left(a^2+b^2\right)\left(c^2+d^2\right)\)
⇔\(a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)=\left(a^2+b^2\right)\left(c^2+d^2\right)\)
⇔\(\left(a^2+b^2\right)\left(c^2+d^2\right)=\left(a^2+b^2\right)\left(c^2+d^2\right)\) ⇒ \(\left(dpcm\right)\)
\(2\)/
⇔\(\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2\ge\left(ac\right)^2+2abcd+\left(bd\right)^2\)
⇔\(\left(ad\right)^2-2abcd+\left(bc\right)^2\ge0\)
⇔\(\left(ad-bc\right)^2\ge0\left(đúng\right)\)
19 tháng 2 2022
a: \(VT=a^2c^2+2abcd+b^2d^2+a^2d^2-2abcd+b^2c^2\)
\(=a^2c^2+a^2d^2+b^2d^2+b^2c^2\)
\(=a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)\)
\(=\left(c^2+d^2\right)\left(a^2+b^2\right)\)
b: Bạn ghi lại đề đi bạn
18 tháng 2 2022
a: \(\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(=a^2c^2+b^2d^2-2abcd+a^2d^2-2abcd+b^2c^2\)
\(=a^2c^2+a^2d^2+b^2d^2+b^2c^2\)
\(=\left(c^2+d^2\right)\left(a^2+b^2\right)\)
b: \(\left(ac+bd\right)^2< =\left(a^2+b^2\right)\left(c^2+d^2\right)\)
\(\Leftrightarrow a^2c^2+2abcd+b^2d^2-a^2c^2-a^2d^2-b^2c^2-b^2d^2< =0\)
\(\Leftrightarrow-a^2d^2+2abcd-b^2c^2< =0\)
\(\Leftrightarrow\left(ad-bc\right)^2>=0\)(luôn đúng)
R
18 tháng 2 2022
a) \(\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(=a^2c^2+2abcd+b^2d^2+a^2d^2-2adbc+b^2c^2\)
\(=a^2c^2+b^2d^2+a^2d^2+b^2c^2\)
\(=\left(a^2c^2+a^2d^2\right)+\left(b^2d^2+b^2c^2\right)\)
\(=a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)\)
\(=\left(a^2+b^2\right)\left(c^2+d^2\right)\)
b) \(\left(a^2+b^2\right)\left(c^2+d^2\right)-\left(ac+bd\right)^{^2}\)
\(=a^2c^2+a^2d^2+b^2c^2+b^2d^2-a^2c^2-2abcd-b^2d^2\)
\(=a^2d^2+b^2c^2-2abcd\)
\(=\left(ad\right)^2-2ad.bc+\left(bc\right)^2\)
\(=\left(ad-bc\right)^2\ge0\)
\(=\left(ac+bd\right)^2\le\left(a^2+b^2\right)\left(c^2+d^2\right)\)
CM
0
