Nếu phương trình 3x2+5y =28 có nghiệm nguyên ( x0; y0) thì x0 chia 5 có số dư là?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LA
2
TN
1
KK
6
KK
1
12 tháng 2 2017
3x2 + 5y = 28
=> 3x2 ≤ 28
=> x2 ≤ 9
=> x ≤ 3
Xét x = 0 => 5y = 28 ( loại )
Xét x = 1 => 3 + 5y = 28 => y = 5
Vì 1 chia 5 dư 1 => x0 chia 5 dư 1
BH
0
TN
1
13 tháng 2 2017
pt: \(9.3^x+5y=28\Leftrightarrow10.3^x+5y-3^x=28\)
Ta thấy: \(10.3^x+5y⋮5\)Mà 28 chia 5 dư 3 => \(3^x\):5 dư 3
xét các chữ số tận cùng của \(3^x\)là: 1,3,7,9 => \(3^x\)phải có tận cùng là 3 => x=4k+1
đoạn sau tự giải quyết nốt nhé!
CM
14 tháng 2 2017
Chọn D.
Phương trình 
Mà x0 là nghiệm của phương trình log3( x + 7a) = 2log2x nên suy ra
log3( x + 7a) = 2log2x tương đương log3( x +7a) = 2
do đó; 7a + 2 = 32
suy ra a = 1.
TV
0
CM
30 tháng 9 2018
Điều kiện: x ≥ 5 3
* ( 10 x + 1 − 9 x + 4 ) + ( 3 x − 5 − 2 x − 2 ) = 0
⇔ 10 x + 1 − ( 9 x + 4 ) 10 x + 1 + 9 x + 4 + 3 x − 5 − ( 2 x − 2 ) 3 x − 5 + 2 x − 2 = 0
⇔ ( x − 3 ) 1 10 x + 1 + 9 x + 4 + 1 3 x − 5 + 2 x − 2 = 0
Vì ∀ x ≥ 5 3 ⇒ ⇔ 1 10 x + 1 + 9 x + 4 + 1 3 x − 5 + 2 x − 2 > 0 nên 1 ⇔ x = 3
Kết hợp điều kiện phương trình có nghiệm duy nhất x = 3
Đáp án cần chọn là: C
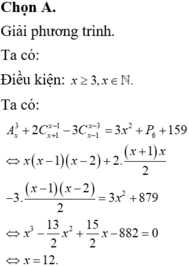
1 chắc 100% luôn
1