\(C_{14}^k+C_{14}^{k+2}=2C_{14}^{k+1}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Theo nhị thức Newton:
$C^k_{2016}$ chính là hệ số của $x^k$ trong khai triển $(x+1)^{2016}(*)$
Lại có:
$(x+1)^{2016}=(x+1)^5.(x+1)^{2011}$
\(=(\sum \limits_{i=0}^5C^i_5x^i)(\sum \limits_{j=0}^{2011}C^i_{2011}x^j)\)
Hệ số $x^k$ trong khai triển này tương ứng với $0\leq i\leq 5; 0\leq j\leq 2011$ thỏa mãn $i+j=k$
Hay hệ số của $x^k$ trong khai triển $(x+1)^{2016}$ là:
$C^0_5.C^k_{2011}+C^1_5.C^{k-1}_{2011}+C^2_5C^{k-2}_{2011}+C^3_5.C^{k-3}_{2011}+C^4_5.C^{k-4}_{2011}+C^5_5.C^{k-5}_{2011}(**)$
Từ $(*); (**)$ ta có đpcm.

sử dụng ct tổng quát (1+x)n thay n=10 và x=2 ta có
(1+2)10=310

Xét khai triển:
\(\left(1+x\right)^{90}=C_{90}^0+C_{90}^1x+C_{90}^2x^2+...+C_{90}^{90}x^{90}\)
Thay \(x=2\) ta được:
\(3^{90}=C_{90}^0+2C_{90}^1+2^2C_{90}^2+...+2^{90}C_{90}^{90}\)
Vậy \(B=3^{90}\)
Mod cho em hỏi cái này với ạ
uy tắc tam đoạn luận : \(\dfrac{\left(p\rightarrow q\right)\curlywedge p}{.\cdot.q}\)
Cho em hỏi ý nghĩa ký tự suy ra và ký tự 3 chấm với ạ

1/ \(2C^k_n+5C^{k+1}_n+4C^{k+2}_n+C^{k+3}_n\)
\(=2\left(C^k_n+C_n^{k+1}\right)+3\left(C^{k+1}_n+C^{k+2}_n\right)+\left(C^{k+2}_n+C^{k+3}_n\right)\)
\(=2C_{n+1}^{k+1}+3C_{n+1}^{k+2}+C_{n+1}^{k+3}\)
\(=2\left(C_{n+1}^{k+1}+C_{n+1}^{k+2}\right)+\left(C_{n+1}^{k+2}+C^{k+3}_{n+1}\right)\)
\(=2C_{n+2}^{k+2}+C_{n+2}^{k+3}=C_{n+2}^{k+2}+\left(C_{n+2}^{k+2}+C_{n+2}^{k+3}\right)=C_{n+2}^{k+2}+C_{n+3}^{k+3}\)
Áp dụng ct:C(k)(n)=C(k)(n-1)+C(k-1)(n-1) có:
................C(k-1)(n-1)= C(k)(n) - C(k)(n-1)
tương tự: C(k-1)(n-2)= C(k)(n-1) - C(k)(n-2)
................C(k-1)(n-3)= C(k)(n-2) -C(k)(n-3)
.........................................
................C(k-1)(k-1)= C(k)(k) (=1)
Cộng 2 vế vào với nhau...-> đpcm

Ta có: \((C_{15}^{12} + C_{15}^{13} )+ C_{16}^{14} = C_{16}^{13} + C_{16}^{14} = C_{17}^{14} = 680\)

a) \(C_7^2 = \frac{{7!}}{{2!.5!}} = \frac{{7.6}}{2} = 21\)
b) \(C_9^0 + C_9^9 = \frac{{9!}}{{0!.9!}} + \frac{{9!}}{{9!.0!}} = 2\)
c) \(C_{15}^3 - C_{14}^3 = \frac{{15!}}{{3!.12!}} - \frac{{14!}}{{3!.11!}} = \frac{{15.14.13}}{{3.2.1}} - \frac{{14.13.12}}{{3.2.1}} = 91\)

a) Để tính \(A_{15}^{10}\) ta ấn liên tiếp các phím
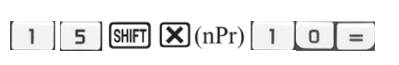
Thì nhận được kết quả là \(1,{08972864.10^{10}}\)
b) Để tính \(C_{10}^6 + C_{10}^7 + C_{11}^8\) thì ta ấn liên tiếp các phím

Thì ta nhận được kết quả là 495
c) Để tính \(C_5^1C_{20}^2 + C_5^2C_{20}^1\) thì ta ấn liên tiếp các phím

Thì ta được kết quả là 1150

\(C_{14}^k+C_{14}^{k+2}=2C_{14}^{k+1}\)
\(\Leftrightarrow\dfrac{14!}{\left(14-k\right)!k!}+\dfrac{14!}{\left(12-k\right)!\left(k+2\right)!}=\dfrac{2.14!}{\left(13-k\right)!\left(k+1\right)!}\)
\(\Leftrightarrow\dfrac{14!}{k!\left(12-k\right)!}\left[\dfrac{1}{\left(14-k\right)\left(13-k\right)}+\dfrac{1}{\left(k+1\right)\left(k+2\right)}\right]=\dfrac{2}{\left(13-k\right)\left(k+1\right)}.\dfrac{14!}{k!\left(12-k\right)!}\)
\(\Leftrightarrow\dfrac{2k^2-24k+184}{\left(14-k\right)\left(k+2\right)\left(13-k\right)\left(k+1\right)}=\dfrac{2}{\left(13-k\right)\left(k+1\right)}\)
\(\Leftrightarrow\dfrac{k^2-12k+92}{-k^2+12k+28}=1\)
\(\Leftrightarrow k^2-12k+92=-k^2+12k+28\)
\(\Leftrightarrow k^2-12k+32=0\)
\(\Leftrightarrow\left[{}\begin{matrix}k=4\\k=8\end{matrix}\right.\)
đề bảo là cm hay tìm k