Giải phương trình :
a) 2x4-x3-9x2+13x-5=0
b) x4-2x3-11x2+12x+36=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
Giải phương trình
e) x4 -4x3-8x2+8x=0
f) 2x2+3xy+y2=0
g) 2x4-x3-9x2+13x-5=0
h) (x+1)(x+3)(x+5)(x+7)+15=0
1
18 tháng 8 2023
e: =>x(x^3-4x^2-8x+8)=0
=>x[(x^3+8)-4x(x+2)]=0
=>x(x+2)(x^2-2x+4-4x)=0
=>x(x+2)(x^2-6x+4)=0
=>\(x\in\left\{0;-2;3+\sqrt{5};3-\sqrt{5}\right\}\)
g: =>2x^4+5x^3-6x^3-15x^2+6x^2+15x-2x-5=0
=>(2x+5)(x^3-3x^2+3x-1)=0
=>(2x+5)(x-1)^3=0
=>x=1 hoặc x=-5/2
h: =>(x^2+8x+7)(x^2+8x+15)+15=0
=>(x^2+8x)^2+22(x^2+8x)+120=0
=>(x^2+8x+10)(x^2+8x+12)=0
=>(x^2+8x+10)(x+2)(x+6)=0
=>\(x\in\left\{-2;-6;-4+\sqrt{6};-4-\sqrt{6}\right\}\)
CM
31 tháng 1 2019
a) Đa thức thương x 2 – 6x + 9.
b) Đa thức thương 2 x 2 – 5.
c) Đa thức thương x 2 + 4x + 3 và đa thức dư -12.
d) Đa thức x + 5 và đa thức dư x – 4.
DT
18 tháng 2 2022
a, \(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)-\left(3x+2\right)\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(\left(9x^2-4\right)-\left(\left(3x+2\right)\left(x-1\right)\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-\left(3x^2-x-2\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-3x^2+x+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)=0;3x^2+x-2=0\)
=> x=-1
với \(3x^2+x-2=0\)
ta sử dụng công thức bậc 2 suy ra : \(x=\dfrac{2}{3};x=-1\)
Vậy ghiệm của pt trên \(S\in\left\{-1;\dfrac{2}{3}\right\}\)
18 tháng 2 2022
b: \(\Leftrightarrow x^2-2x+1-1+x^2=x+3-x^2-3x\)
\(\Leftrightarrow2x^2-2x=-x^2-2x+3\)
\(\Leftrightarrow3x^2=3\)
hay \(x\in\left\{1;-1\right\}\)
c: \(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x-3\right)-\left(x-1\right)\left(x-2\right)\left(x+2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[\left(x+1\right)\left(x-3\right)-\left(x-2\right)\left(x+5\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-2x-3-x^2-3x+10\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(-5x+7\right)=0\)
hay \(x\in\left\{1;-2;\dfrac{7}{5}\right\}\)
CM
24 tháng 12 2019
+Trước tiên từ đồ thị hàm số y= 2x3- 9x2+12x , ta suy ra đồ thị hàm số y= 2 x 3 - 9 x 2 + 12 x như hình dưới đây:
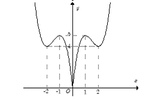
+ Phương trình 2 x 3 - 9 x 2 + 12 x + m = 0 và đường thẳng y= -m
+ Dựa vào đồ thị hàm số y = 2 x 3 - 9 x 2 + 12 x , yêu cầu bài toán trở thành:
4< -m< 5 hay -5<m< -4.
Chọn B.
10 tháng 8 2021
d: Ta có: \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)=24\)
\(\Leftrightarrow\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24=0\)
\(\Leftrightarrow x\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
CM
7 tháng 7 2019
Cả ba phương trình trên đều là phương trình trùng phương.
a) 3 x 4 – 12 x 2 + 9 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 3 t 2 – 12 t + 9 = 0 ( 2 )
Giải (2):
Có a = 3; b = -12; c = 9
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 v à t 2 = 3 .
Cả hai nghiệm đều thỏa mãn điều kiện.
+ t = 3 ⇒ x 2 = 3 ⇒ x = ± 3 + t = 1 ⇒ x 2 = 1 ⇒ x = ± 1
Vậy phương trình có tập nghiệm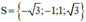 
b) 2 x 4 + 3 x 2 – 2 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 2 t 2 + 3 t – 2 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 3 ; c = -2
⇒ Δ = 3 2 – 4 . 2 . ( - 2 ) = 25 > 0
⇒ (2) có hai nghiệm
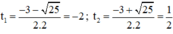
t 1 = - 2 < 0 nên loại.
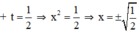
Vậy phương trình có tập nghiệm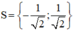 
c) x 4 + 5 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , t > 0 .
(1) trở thành: t 2 + 5 t + 1 = 0 ( 2 )
Giải (2):
Có a = 1; b = 5; c = 1
⇒ Δ = 5 2 – 4 . 1 . 1 = 21 > 0
⇒ Phương trình có hai nghiệm:
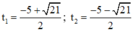
Cả hai nghiệm đều < 0 nên không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 5 2021
Đặt \(f\left(x\right)=2x^3-9x^2+12x-2-m\)
\(f\left(x\right)\) là hàm đa thức nên liên tục trên R
\(\forall m\in\left(2;3\right)\) ta có:
\(f\left(0\right)=-2-m< 0\)
\(f\left(1\right)=3-m>0\)
\(\Rightarrow f\left(0\right).f\left(1\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;1\right)\) (1)
\(f\left(2\right)=2-m< 0\)
\(\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\) (2)
\(f\left(3\right)=7-m>0\)
\(\Rightarrow f\left(2\right).f\left(3\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(2;3\right)\) (3)
Từ (1); (2); (3) \(\Rightarrow f\left(x\right)\) luôn có 3 nghiệm dương pb
Ví dụ 3: Giải phương trình :
(4).
Giải: Ta có phương trình:
Do vậy
a) Ta có :\(2x^4-x^3-9x^2+13x-5=0=>\left(x-1\right)^3\left(2x+5\right)=0\)
=>\(\left\{\begin{matrix}\left(x-1\right)^3=0\\2x+5=0\end{matrix}\right.=>\left\{\begin{matrix}x-1=0\\2x=-5\end{matrix}\right.=>\left\{\begin{matrix}x=1\\x=-2,5\end{matrix}\right.\)
Vậy tập nghiệm của phương trình S={-2,5 ;1}
b)\(x^4-2x^3-11x^2+12x+36=0=>\left(x-3\right)^2\left(x+2\right)^2=0\)
=>\(\left\{\begin{matrix}\left(x-3\right)^2=0=>x-3=0=>x=3\\\left(x+2\right)^2=0=>x+2=0=>x=-2\end{matrix}\right.\)
Vậy tập nghiệm của pt là S={-2;3}