Giải hệ phương trình tìm nguyên dương
x3 - y3 - z3= 3xyz
x2= 2.(y+z)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 4 2019
M = x 3 + y 3 + z 3 - 3 x y z x 2 + y 2 + z 2 - x y - y z - x z
CM
16 tháng 2 2017
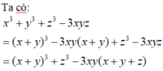
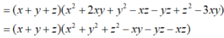
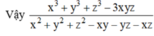
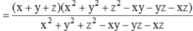
Ta có: x 3 + y 3 = ( x + y ) 2 < = > ( x + y ) ( x 2 − x y + y 2 − x − y ) = 0
Vì x, y nguyên dương nên x+y > 0, ta có: x 2 − x y + y 2 − x − y = 0
⇔ 2 ( x 2 − x y + y 2 − x − y ) = 0 ⇔ x - y 2 + x - 1 2 + ( y - 1 ) 2 = 2
Vì x, y nguyên nên có 3 trường hợp:
+ Trường hợp 1: x − y = 0 x - 1 2 = 1 ⇔ x = y = 2 , z = 4 y - 1 2 = 1
+ Trường hợp 2: x − 1 = 0 x - y 2 = 1 ⇔ x = 1 , y = 2 , z = 3 y - 1 2 = 1
+ Trường hợp 3: y − 1 = 0 x - y 2 = 1 x - 1 2 = 1 ⇔ x = 2 , y = 1 , z = 3
Vậy hệ có 3 nghiệm (1,2,3);(2,1,3);(2,2,4)
CM
6 tháng 9 2019
Cách 1
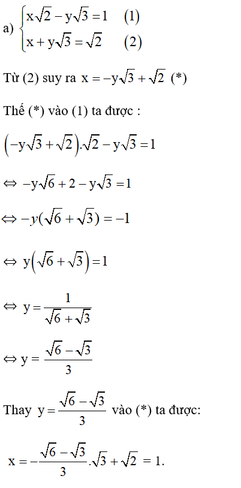
Vậy hệ phương trình có nghiệm duy nhất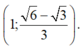 
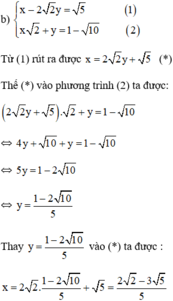
Vậy hệ phương trình có nghiệm duy nhất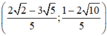 
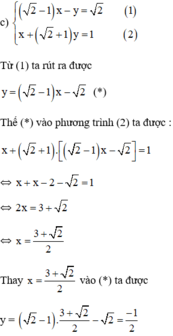
Vậy hệ phương trình có nghiệm duy nhất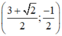 
Cách 2
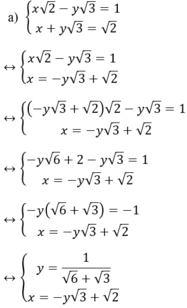
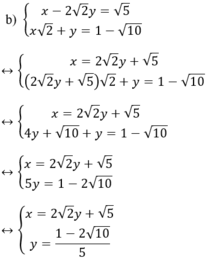
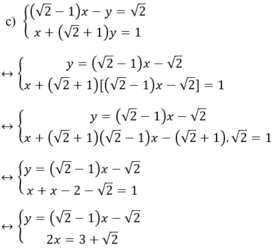
Kiến thức áp dụng
Giải hệ phương trình ta làm như sau:
Bước 1: Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
CC
0
CM
23 tháng 1 2017
Ta có
x 2 − y 3 = 1 x + y 3 = 2 ⇔ x 2 − y 3 = 1 x 2 + y 6 = 2 ⇔ x 2 − y 3 = 1 6 + 3 y = 1 ⇔ x 2 − y 3 = 1 y = 1 6 + 3 ⇔ y = 6 − 3 3 x 2 − 3 . 6 − 3 3 = 1 ⇔ y = 6 − 3 3 x = 1
Vậy hệ đã cho có nghiệm duy nhất ( x ; y ) = 1 ; 6 − 3 3
Đáp án: D
Áp dụng hằng đẳng thức \(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\) với \(a=x,b=-y,c=-z\) ta được \(x^3-y^3-z^3-3xyz=\left(x-y-z\right)\left(x^2+y^2+z^2+xy-yz+zx\right)\) Thành thử \(x=y+z\) hoặc \(x^2+y^2+z^2+xy-yz+zx=0.\) Vì \(x,y,z\) là các số nguyên dương nên \(x^2+y^2+z^2+xy-yz+zx>x^2+z^2-xz\ge xz>0.\) Suy ra \(x=y+z\). Vì \(x^2=2\left(y+z\right)\to x^2=2x\to x=2\to y+z=2\to y=z=1.\) (Vì các số \(x,y,z\) nguyên dương).
Vậy \(\left(x,y,z\right)=\left(2,1,1\right).\)