diện tích hình phẳng giới hạn bởi các đường y=-x^2+2 , y=căn bậc 2 của (1-x^2) và ox là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
.
.
.
.
CM
19 tháng 3 2019
Đáp án A
Phương trình hoành độ giao điểm e x = 2 ⇔ x = ln 2
Suy ra diện tích cần tìm bằng S = ∫ 0 ln 2 e x - 2 d x + ∫ ln 2 0 e x - 2 d x = 4 ln 2 + e - 5 .
CM
9 tháng 6 2019
Chọn B.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = x3 + 3x và y = -x là: x3 + 4x = 0 ⇔ x = 0
Ta có: x3 + 4x ≤ 0, ∀ x ∈ [-2;0].
Do đó:
CM
4 tháng 1 2018
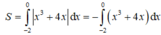
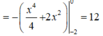
Chọn A.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = 2x - x2 và x + y = 2 là :
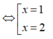
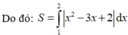
Giữa đồ thị \(y=-x^2+2\) và \(y=\sqrt{1-x^2}\) không có giao điểm chung thì tính diện tích hình giới hạn làm sao được bạn?
không biết nữa thấy đề trên mạng như thế ak mà giả giúp câu này nữa nha x^3-x , x-x^2 tính diện tích hình phẳng giới hạn bởi 2 đường cong