cho tam giác ABC có AB=4cm, điểm D trên cạnh AB sao cho AD=3cm lấy điểm E trên cạnh AC sao cho DE//BC. tính tỉ số giữa AE và AC rồi tính độ dài AE,AC,EC bíêt AE+AC=14cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AP
10 tháng 1 2019
Hình bạn tự vẽ nha
Áp dụng định lý talet trong tam giác ABC ta có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\\ \Leftrightarrow\dfrac{3}{4}=\dfrac{AE}{AC}\\ \Leftrightarrow AC=\dfrac{4AE}{3}\)
\(\text{Mà}AE+AC=14\\ \Rightarrow\dfrac{4AE}{3}+AE=14\\ \Leftrightarrow\dfrac{7AE}{3}=14\\ \Leftrightarrow AE=6\)
⇒AC=12
⇒EC=AC-AE=12-6=6
LD
25 tháng 3 2022
Hình bạn tự vẽ ạ.
a, Xét \(\Delta ADE\) và \(\Delta ABC\) có :
\(\dfrac{AD}{AB}=\dfrac{7}{14}=\dfrac{1}{2}\)
\(\dfrac{AE}{AC}=\dfrac{10}{20}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(=\dfrac{1}{2}\right)\)
Mà \(\widehat{A}:chung\)
\(\Rightarrow\Delta ADE\sim\Delta ABC\left(c-g-c\right)\)
b, Ta có : \(\Delta ADE\sim\Delta ABC\left(cmt\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{ED}{BC}\)
hay \(\dfrac{7}{14}=\dfrac{ED}{18}\)
\(\Rightarrow ED=\dfrac{7.18}{14}=9\left(cm\right)\)
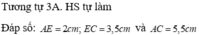
Xét ΔABC có DE//BC
nên AD/AB=AE/AC
=>AE/AC=3/4
=>AE/3=AC/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AE}{3}=\dfrac{AC}{4}=\dfrac{AE+AC}{3+4}=\dfrac{14}{7}=2\)
Do đó: AE=6cm; AC=8cm