Tìm các cặp số nguyên a,b thỏa mãn: ab+2a-3b=11
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có :
\(ab+2a-b=3\)
\(\Leftrightarrow\)\(a\left(b+2\right)-b-2=1\)
\(\Leftrightarrow\)\(a\left(b+2\right)-\left(b+2\right)=1\)
\(\Leftrightarrow\)\(\left(a-1\right)\left(b+2\right)=1\)
Đến đây bạn xét các trường hợp ra
Chúc bạn học tốt

đơn giản
ab+2a-(b+2)=1
<=>a(b+2)-(b+2)=1
<=>(a-1)(b+2)=1=1.1=(-1).(-1)
+)(a-1)(b+2)=1.1
=>a-1=1 và b+2=1
=>a=2 và b=-1
+)(a-1)(b+2)=(-1).(-1)
=>a-1=-1 và b+2=-1
=>a=0 và b=-3
Vậy \(\left(a;b\right)\in\left\{\left(0;-3\right);\left(2;-1\right)\right\}\)


Lời giải:
$ab+11=2a+3b$
$ab-2a-3b+11=0$
$a(b-2)-3(b-2)+5=0$
$(a-3)(b-2)=-5$
Vì $a,b$ là số nguyên nên $a-3, b-2$ là số nguyên. Ta có bảng sau: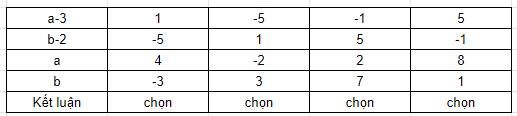


Câu 1:
Ta có: \(2a^2+a=3b^2+b\Rightarrow2a^2+a-3b^2-b=0\Rightarrow3\left(a^2-b^2\right)+\left(a-b\right)=a^2\)
\(\Rightarrow3\left(a-b\right)\left(a+b\right)+\left(a-b\right)=a^2\Rightarrow\left(a-b\right)\left(3a+3b+1\right)=a^2\)
Gọi \(ƯCLN\)\(\left(a-b;3a+3b+1\right)=d\)
=> \(a-b⋮d;3a+3b+1⋮d\Rightarrow\left(a-b\right)\left(3a+3b+1\right)⋮d^2\Rightarrow a^2⋮d^2\Rightarrow a⋮d\Rightarrow6a⋮d\left(1\right)\)
Mà ta lại có: \(3\left(a-b\right)+\left(3a+3b+1\right)⋮d\Rightarrow6a +1⋮d\left(2\right)\)
Từ 1 và 2 => \(d=1\) => \(a-b\) và \(3a+3b+1\) là 2 số nguyên tố cùng nhau.
Và đồng thời \(3a+3b+1>a-b\Rightarrow\begin{cases}3a+3b+1=a^2\\a-b=1^2\end{cases}\)
Vậy \(3a+3b+1\) và \(a-b\) đều là các số chính phương.
Câu 2:
Ta có: \(6x+5y+18=2xy\Rightarrow5y+18=2xy-6x=2x\left(y-3\right)\Rightarrow2x=\frac{5y+18}{y-3}=\frac{5\left(y-3\right)+33}{y-3}=5+\frac{33}{y-3}\)
Do \(x;y\in Z\Rightarrow\)\(\frac{33}{y-3}\in Z\Rightarrow33⋮y-3\Rightarrow y-3\inƯ\left(33\right)=\left\{\pm1;\pm3;\pm11;\pm33\right\}\)
Ta có bảng sau:
| y-3 | 1 | -1 | 3 | -3 | 11 | -11 | 33 | -33 |
| 2x-5 | 33 | -33 | 11 | -11 | 3 | -3 | 1 | -1 |
| 2x | 38 | -28 | 16 | -6 | 8 | 2 | 6 | 4 |
| x | 19 | -14 | 8 | -3 | 4 | 1 | 3 | 2 |
| y | 4 | 2 | 6 | 0 | 14 | -9 | 36 | -30 |
Vậy \(\left(x;y\right)=\left(19;4\right);\left(-14;2\right);\left(8;6\right);\left(-3;0\right);\left(4;14\right);\left(1;-9\right);\left(3;36\right);\left(2;-30\right)\)


a) (x+1)+(x+2)+(x+3)+........+(x+100)=5750
(x+x+...+x)+(1+2+3+...+100)=5750
(x.100)+(1+100).100:2=5750
(x.100)+5050=5750
x.100=5750-5050
x.100=700
x =700:100
x = 7
Vậy x = 7
c) trước hết cần chú ý rằng mọi số tự nhiên đều viết được dưới 1 trong 3 dạng: 3k, 3k +1 hoặc 3k +2(với k là số tự nhiên)
+) Nếu p = 3k vì p là số nguyên tố nên k = 1 => p = 3 => p+10 = 13 là số nguyên tố; p+14 = 17 là số nguyên tố (1)
+) Nếu p = 3k +1 => p +14 = 3k+1+14 = 3k+15 = 3(k+5) chia hết cho 3 và lớn hơn 3 nên là hợp số (loại vì không thỏa mãn điều kiện đề bài) (2)
+) Nếu p=3k+2 => p+10 = 3k+2+10 = 3k+12 = 3(k+4) chia hết cho 3 và lớn hơn 3 nên là hợp số (loại vì không thỏa mẫn điều kiện đề bài) (3)
Từ (1), (2), (3) suy ra p = 3 là giá trị cần tìm.
Vậy nha còn câu b mình tạm thời chưa biết, chúc bạn học tốt
ab+2a-b=3
a(b+2)-b=3
a(b+2)-b+2=3+2
(b+2)(a-1)=5
sau đó bạn tìm các nghiệm cho chúng thỏa mãn nhé(cho là hai số trên thuộc ước của 5 rồi tính)
 Hoàng Phan
Hoàng Phan
\(ab+2a-3b=11\)\(\left(a,b\in Z\right)\)
\(\Rightarrow ab+2a-3b-6=11-6\)
\(\Rightarrow ab+2a-\left(3b+6\right)=5\)
\(\Rightarrow ab+2a-\left(3b+3\times2\right)=5\)
\(\Rightarrow a\left(b+2\right)-3\left(b+2\right)=5\)
\(\Rightarrow\left(a-3\right)\left(b+2\right)=5\)
\(\Rightarrow\left(a-3\right)\left(b+2\right)=\left(-1\right)\times\left(-5\right)=\left(-5\right)\times\left(-1\right)=1\times5=5\times1\)
Ta có bảng sau:
mà \(a,b\in Z\)
\(\Rightarrow\) Các cặp số \(\left(a,b\right)\) thỏa mãn là \(\left(2;-7\right),\left(-2;-3\right),\left(4;3\right)\) và \(\left(8;-1\right)\).
Vậy các cặp số \(\left(a;b\right)\) thỏa mãn đề bài là \(\left(2;-7\right),\left(-2;-3\right),\left(4;3\right)\) và \(\left(8;-1\right)\).