
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 11:
a. $2x^3(x^2-3x+4)=2x^5-6x^4+8x^3$
b. $(x+3)(x-5)=x^2-5x+3x-15=x^2-2x-15$
c. $(x+5)^2-(x+4)(x-4)=x^2+10x+25-(x^2-16)$
$=10x+41$
Câu 12:
a.
$x^2-3xy=x(x-3y)$
b.
$x^2+6x+9-y^2=(x^2+2.x.3+3^2)-y^2=(x+3)^2-y^2$
$=(x+3-y)(x+3+y)$

Bài 6:
Phương trình hoành độ giao điểm là:
\(ax^2+4x+4=0\)
\(\text{Δ}=16-16a\)
Để (P) tiếp xúc với (d) thì 16-16a=0
hay a=1





Bài 1:
a) Ta có: \(B=\dfrac{x}{\sqrt{x}-1}-\dfrac{2x-\sqrt{x}}{x-\sqrt{x}}\)
\(=\dfrac{x}{\sqrt{x}-1}-\dfrac{\sqrt{x}\left(2\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}-1}=\sqrt{x}-1\)

\(m\left(2m-3\right)-2m\left(m+1\right)\)
\(=2m^2-3m-2m^2-2m=-5m⋮5\Rightarrow dpcm\)
\(m\left(2m-3\right)-2m\left(m+1\right)\)
\(=2m^2-3m-2m^2-2m\)
\(=-5m⋮5\) \(\forall m\in Z\)
Vậy \(m\left(2m-3\right)-2m\left(m+1\right)⋮m\left(\forall m\in Z\right)\)







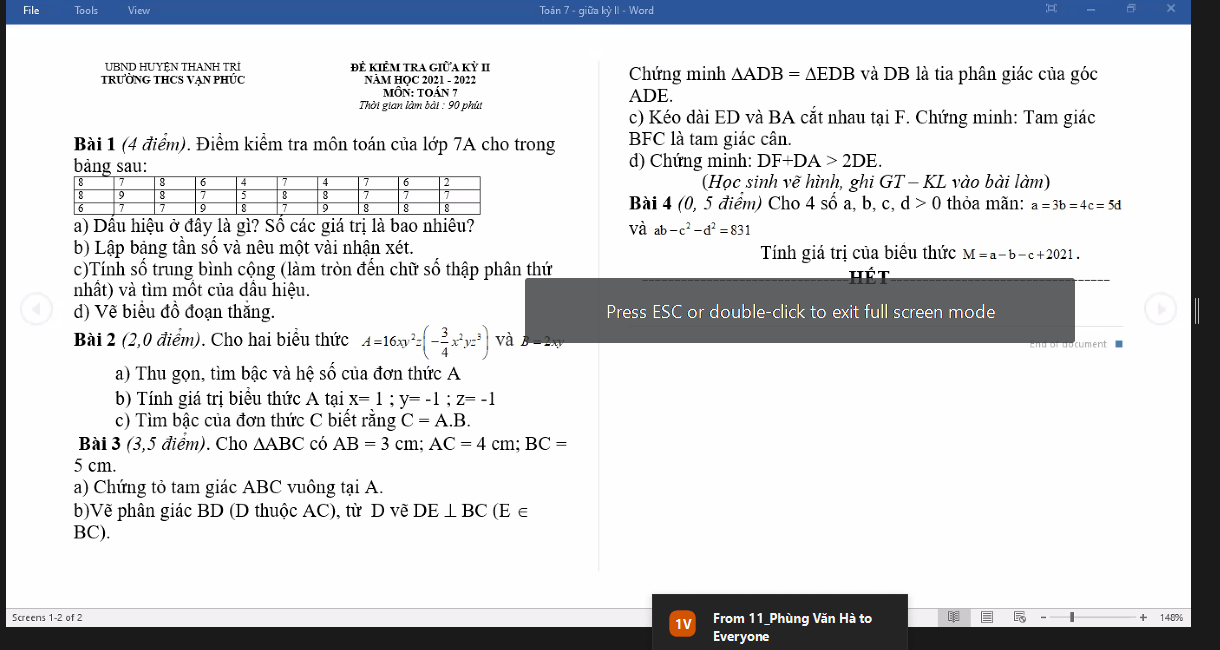
 giúp minh với
giúp minh với
\(A=\left(1-\frac{\sqrt{x}}{1+\sqrt{x}}\right)\div\left(\frac{\sqrt{x}+3}{\sqrt{x}-2}+\frac{\sqrt{x}+2}{3-\sqrt{x}}+\frac{\sqrt{x}+2}{x-5\sqrt{x}+6}\right)\)(ĐK: \(x\ge0,x\ne4,x\ne9\))
\(=\frac{1+\sqrt{x}-\sqrt{x}}{1+\sqrt{x}}\div\frac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\frac{1}{1+\sqrt{x}}\times\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}{\sqrt{x}-3}=\frac{\sqrt{x}-2}{\sqrt{x}+1}\)
\(A< \frac{1}{2}\Leftrightarrow\frac{\sqrt{x}-2}{\sqrt{x}+1}< \frac{1}{2}\)(\(x\ge0,x\ne4,x\ne9\))
\(\Leftrightarrow\frac{2\sqrt{x}-4-\left(\sqrt{x}+1\right)}{2\left(\sqrt{x}+1\right)}< 0\)
\(\Leftrightarrow\sqrt{x}-5< 0\)
\(\Leftrightarrow x< 25\).
Vậy \(0\le x< 25,x\ne4,x\ne9\)thì \(A< \frac{1}{2}\).
\(A=\frac{\sqrt{x}-2}{\sqrt{x}+1}=\frac{\sqrt{x}+1-3}{\sqrt{x}+1}=1-\frac{3}{\sqrt{x}+1}\inℤ\Leftrightarrow\frac{3}{\sqrt{x}+1}\inℤ\)
suy ra \(\sqrt{x}+1\inƯ\left(3\right)=\left\{1,3\right\}\)vì \(x\inℤ\)
\(\Rightarrow x\in\left\{0,4\right\}\)
Đối chiếu điều kiện ta chỉ có \(x=0\)thỏa mãn.