Giai phương trình trên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


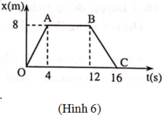
a) Giai đoạn 1: v 1 = x A − x 0 t A − t 0 = 8 4 = 2 m/s.
Giai đoạn 2: v 2 = x B − x A t B − t A = 0 (vật dừng lại).
Giai đoạn 3: v 3 = x C − x B t C − t B = 0 − 8 16 − 12 = − 2 m/s.
b) Phương trình chuyển động trong các giai đoạn:
Giai đoạn 1: x 1 = 2 t (m); Điều kiện 0 < t < 4.
Giai đoạn 2: x 2 = 8 ( m ) = hằng số; Điều kiện 4 < t < 12.
Giai đoạn 3: x 3 = 8 − 2 t (m); Điều kiện 12 < t < 20.
c) Quãng đường đi trong 16 giây đầu tiên: s = v 1 t 1 + v 3 t 3 = 2.4 + 2.4 = 16 m.

\((C_6H_{10}O_5)_n + nH_2O \xrightarrow{H^+} nC_6H_{12}O_6\\ C_6H_{12}O_6 \xrightarrow{men\ rượu,30^0-35^o}2CO_2 + 2C_2H_5OH\)
Theo PTHH :
\(n_{C_6H_{12}O_6} = n.n_{tinh\ bột\ pư} = n.\dfrac{100}{162n}.80\%= \dfrac{40}{81}mol\)
\(n_{C_6H_{12}O_6\ pư} = \dfrac{40}{81}.75\% = \dfrac{10}{27}mol\\ \Rightarrow n_{C_2H_5OH} = 2n_{C_6H_{12}O_6\ pư} = 2. \dfrac{10}{27}= \dfrac{20}{27}mol\\ \Rightarrow m_{C_2H_5OH} = \dfrac{20}{27}.46 = 34,074(kg)\)


1.
\(-5x+3\ge0\)
\(\Leftrightarrow-5x\ge-3\)
\(\Rightarrow x\le\dfrac{3}{5}\)
2.
\(3x-5>2x+1\)
\(\Leftrightarrow3x-2x>1+5\)
\(\Rightarrow x>6\)
3.
\(8x+4\ge3x+19\)
\(\Leftrightarrow8x-3x\ge19-4\)
\(\Leftrightarrow5x\ge15\)
\(\Rightarrow x\ge3\)
4.
\(3x-8\ge5x\)
\(\Leftrightarrow3x-5x\ge8\)
\(\Leftrightarrow-2x\ge8\)
\(\Rightarrow x\le-4\)
1)
`-5x+3≥0`
`<=>-5x≥-3`
`<=>-5x*(-1)/5≤3*(-1)/5`
`<=>x≤3/5`
2)
`3x-5>2x+1`
`<=>3x-2x>1+5`
`<=>x>6`
3)
`8x+4≥3x+19`
`<=>8x-3x≥19-4`
`<=>5x≥15`
`<=>5x*1/5≥15*1/5`
`<=>x≥3`
4)
`3x-8≥5x`
`<=>3x-5x≥8`
`<=>-2x≥8`
`<=>-2x*(-1)/2≤8*(-1)/2`
`<=>x≤-4`

a) \(x^4-13x^2+36=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)\left(x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\\x=-2\\x=-3\end{matrix}\right.\)
b) \(5x^4+3x^2-8=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(5x^2+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)( do \(5x^2+8\ge8>0\))
c: Ta có: \(2x^4+3x^2+2=0\)
Đặt \(a=x^2\)
Phương trình tương đương là: \(2a^2+3a+2=0\)
\(\text{Δ}=3^2-4\cdot2\cdot2=9-16=-7\)
Vì Δ<0 nên phương trình vô nghiệm
Vậy: Phương trình \(2x^4+3x^2+2=0\) vô nghiệm
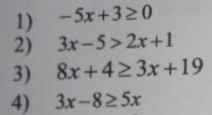


Đặt \(x^2=t\left(t\ge0\right)\) khi đó pt tương đương với
\(t^2+\left(\sqrt{2}+1\right)t-\left(\sqrt{2}+2\right)\)
\(\Delta=\left(\sqrt{2}+1\right)^2+4\left(\sqrt{2}+2\right)\)\(=11+6\sqrt{2}\)
Ta thấy denta lớn hơn 0 nên có 2 nghiệm phân biệt là
\(t_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-\left(\sqrt{2}+1\right)+\sqrt{11+6\sqrt{2}}}{2}=1\)
\(t_2=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-\left(\sqrt{2}+1\right)-\sqrt{11+6\sqrt{2}}}{2}=-2-\sqrt{2}\left(ktmđk\right)\)
Ta có: \(t_1=1\Leftrightarrow\left[\begin{matrix}x_1=1\\x_2=-1\end{matrix}\right.\)
Vậy pt đã cho có 2 nghiệm là 1 và -1
nên tang vào toàn math thi giải tốt hơn bạn